Algebraic Proof

L.O To be able to determine whether a statement is true or false through algebraic explanation.

Simplifying, factorising and solving numerical problems are only one aspect of algebra. The test of true algebraic understanding is using it to prove different concepts and mathematical statements.

A few Algebraic expressions you should know :

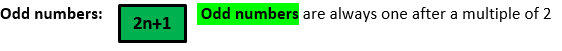
Notice how they both have 1,2 and 3 after the same starting terms of n or 2n. n is usually used as it is a simpler term.

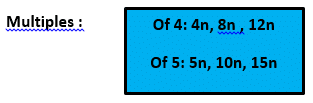
Notice how they both have multiples of the specified number before n. They also go up in a linear orderr multiples so they are consecutive.

Example 1:

Prove if the sum of any 3 consecutive integers is a multiple of 3.

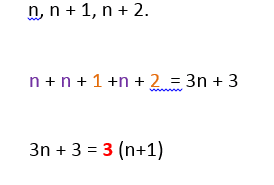
So, the sum of any 3 consecutive numbers where n + 1 is an integer will always be a multiple of 3.

Example 2:

Prove if the sum of 4 consecutive odd numbers is a multiple of 8.

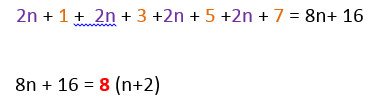
So, the sum of any 4 consecutive odd numbers, where n + 2 is an integer will always be a multiple of 8.

Example 3:

Prove that the sum of the squares of 2 consecutives even numbers is never a multiple of 8.

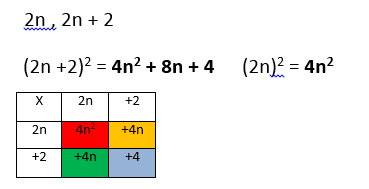
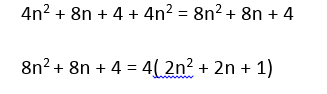
Here the sum of the squares of 2 consecutive even numbers is never a multiple of 8.

Example 4:

Prove that if you have 2 consecutive even numbers, if they are squared and you find the difference, it is the same as adding the two numbers and multiplying the total sum by 2.

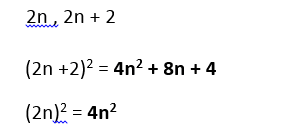
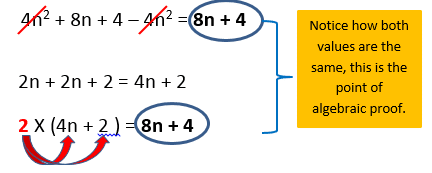
Here both values are the same hence multiplying the sum of 2 consecutive even numbers acquires the same value after squaring and finding the difference.