Area and Perimeter

---

L.O – To be able to calculate the area of rectangles, triangles, parallelograms, trapeziums and also more complex shapes.

Area of a rectangle

The formula for the area of a rectangle is:

Area = base x height

A = b x h

Example 1:

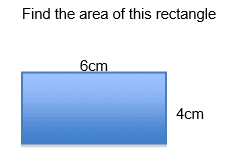
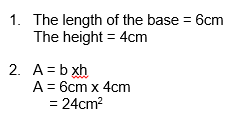
Steps:

1. Identify the length of the base and the height of the rectangle.
2. Using the formula, A= b x h, substitute b and h for the values identified in step 1.Remember units! For area always add a  ² , e.g. cm², m², km² etc

Area of a triangle

The formula for the area of a triangle is:

Area = ¹/₂ × base × height

A = ¹/₂ x b x h

The height used must be the perpendicular height! This is especially important is you are not given a right angled triangle.

Steps:

1. Identify the length of the base and the height of the triangle.
2. Using the formula, A=¹/₂ x b x h, substitute b and h for the values identified in step 1.

 

Example 1:

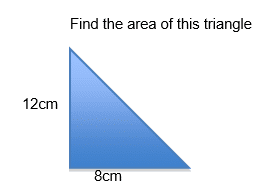
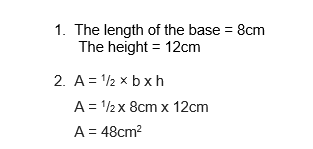
Steps:

1. Split the shape up into simpler shapes e.g. triangles, squares and rectangles Draw each shape out separately and label the lengths of the sides (base and heights).You may need to work out some new lengths using the diagram and the lengths given.
2. Find the area of each of the separate shapes.
3. Add the areas of the separate shapes together. This will give you the area of the complex shape!

Area of complex shapes

Sometimes, you will have to split up a complex shape into smaller shapes. You find the area of these smaller shapes and add them up to find the area of the original shape.

Example 1:

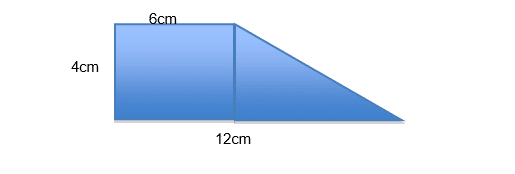
1.The two shapes that this complex shape is made up of

 

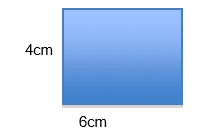
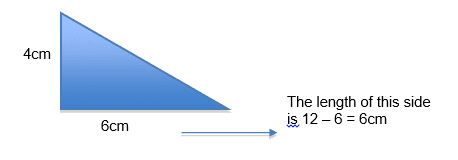
2.Area of rectangle = 4 x 6 = 24cm²

Area of triangle = ½ x 4 x 6 = 12cm²

3.Total area of complex shape = area of rectangle + area of triangle

=24cm² + 12cm²

= 36cm²

 

Steps:

1. Split the shape up into simpler shapes e.g. triangles, squares and rectangles Draw each shape out separately and label the lengths of the sides (base and heights).You may need to work out some new lengths using the diagram and the lengths given.
2. Find the area of each of the separate shapes.
3. Add the areas of the separate shapes together. This will give you the area of the complex shape!

 

Area of a parallelogram

The formula for area of a parallelogram is;

Area  = base x perpendicular height

A = b x h

It is really important that you use the perpendicular height and not just the height of one of the slanted sides for h!

Example 1:

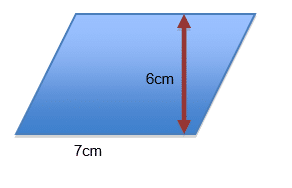
1. The length of the base = 7cm

The perpendicular height = 6cm

2. A = b x h

= 7cm x 6cm

= 42cm²

 

 

Steps:

1. Identify the length of the base and the perpendicular height of the parallelogram.
2. Using the formula, A= b x h, substitute b and h for the values identified in step 1. Remember units!

Don’t forget à use perpendicular height!

Area of a trapezium

The formula for the area of a trapezium is;

A = ¹/₂ × h × (a + b)

You must use the perpendicular height!

a and b are the lengths of the two parallel sides of the trapezium. It doesn’t matter which length is a/b.

Example 1:

 

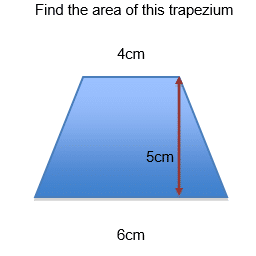
1. Length of the base = 6cm

Perpendicular height = 5cm

Length of a = 4cm

Length of b = 6cm

2. A = ¹/₂ × h × (a + b)

A = ½ x 5cm x (4cm +6cm)

A = 25cm²

 

 

Perimeter

 The perimeter of a shape is the distance around it.

To work out the perimeter, all you have to do is add all of the sides of the shape together!

If you are given a complex shape, you may have to work out the length of some of the sides before you can find the perimeter.

Steps:

1. Identify the length of the base and the height of the triangle.Also identify the lengths of the two parallel sides of the trapezium, a and b.
2. Using the formula, A = ¹/₂ × h × (a + b), substitute b, h, a and b for the values identified in step 1.