Congruence and Similarity

---

Congruence

Congruence = same, therefore if two shapes are congruent, they are the same shape and the same size. Shapes can be congruent even if one of them has been reflected or rotated.

Here are two sets of congruent shapes

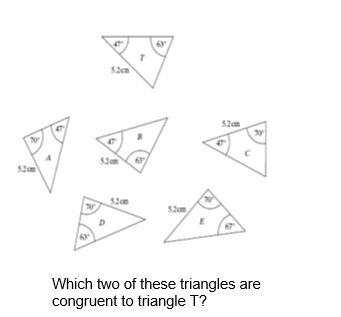
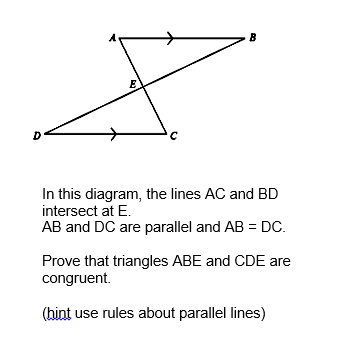
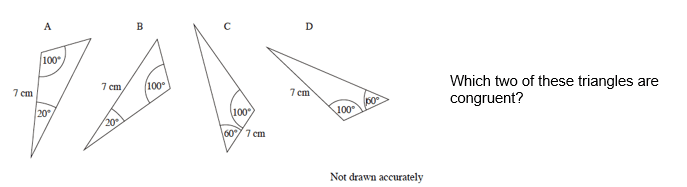
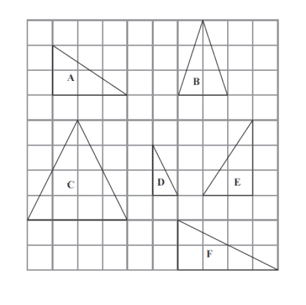
You are likely to be given two triangles and asked to determine whether they are congruent or not.

In order for two triangles to be congruent they must meet one (or more) of these conditions;

• Side Side Side Rule (SSS) – all 3 sides are the same

 

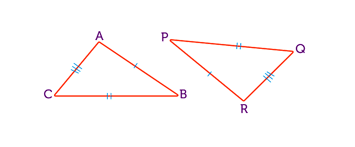
• Angle Angle Side Rule (AAS) – two angles and a side are the same

 

 

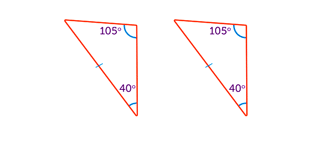
• Side Angle Side Rule (SAS) – two sides and the angle between them is the same

 

 

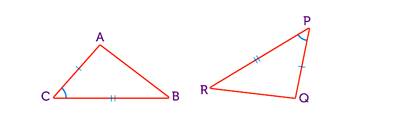
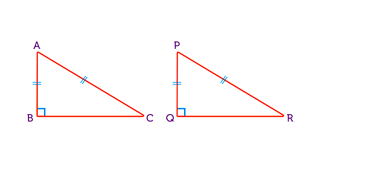
• RHS – a right angle, the hypotenuse (longest side) and one other side are the same

 

If one of these conditions is met, the triangles are congruent. Note – not all the conditions have to be true!

Tips:

• Two triangles which have the same 3 angles may not be congruent, as they can have different sides
• In order to determine whether two triangles fit any of the above rules, draw them out in the same orientation (position). This will reduce your chance of getting confused and making silly mistakes.

 

In the diagram, the sides which are marked with one dash are equal. Similarly, the sides which are marked with two dashes are equal etc.

Using the same method, the angles marked with one arc are equal as are the angles which are marked with two arcs and the angles which are marked with three arcs.

Example 1:

Are these triangles congruent? Give a reason for your answer

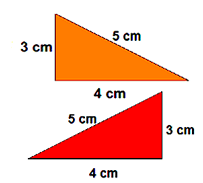
Yes, the triangles are congruent because the following condition is met ‘all 3 sides are the same – (SSS) rule’

Example 2:

Which triangles show below are congruent?

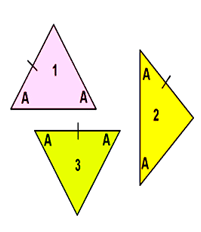
• Triangles 1 and 3 are congruent because they both meet this condition ‘two angles and a side are the same – (AAS) rule’
• Triangle 2 is not congruent because its sides are clearly longer than the other two triangles. Remember congruent = same shape and size!

Similarity

Similar = same shape, different size.

 Two triangles are similar if;

• all the pairs of angles are the same
• all the pars of sides are proportional

In order for two triangles to be similar they must meet one of these conditions;

• Angle Angle Rule (AA) – any two angles must be the same

• Side Side Side Rule (SSS) – all three side lengths are proportional

 

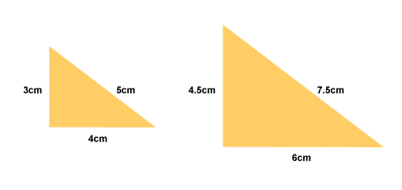
All the lengths in the second triangle are 1.5 times the lengths in the first triangle. Hence, the 3 sides are in the same proportion.

Side Angle Side Rule (SAS) – two sides are proportional and the angle between them is the same.

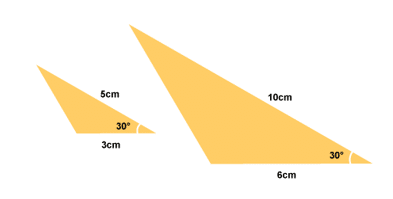
The two given lengths in the second triangle are double the corresponding lengths in the first triangle. Hence, the sides are proportional.

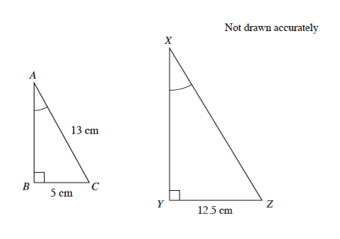
Example 1:

Find the lengths AB and EF, given that these triangles are similar

 

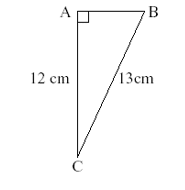
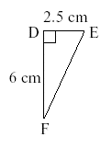
First we need to find the scale factor. Using lengths AC(12cm) and DF(6cm) we can work out that the scale factor is 0.5 ( all the legnths in the triangle DEF are half those in triangle ABC

Length AB = 5cm (double DE)

Length EF = 6.5cm (half BC)

Example 2:

Find the lengths EG and FG

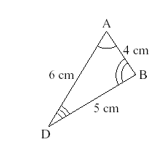
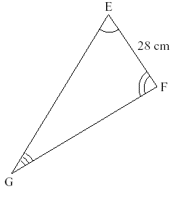
 The scale factor is 7

Length EG = 6 x 7 = 42cm

Length FG = 5 x 7 = 35cm

Be careful when deciding whether to multiply/divide by the scale factor!

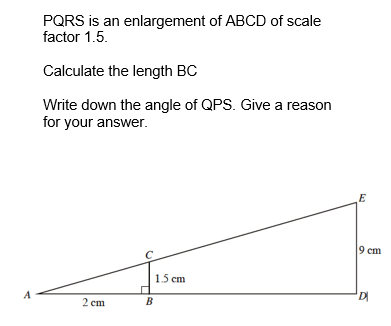
Example 3:

If you are struggling, just look at whether the side your finding is on the ‘little’ shape or ‘big’ shape. If it is on the bigger shape, you need to obviously multiply, if on the smaller shape, you need to divide.

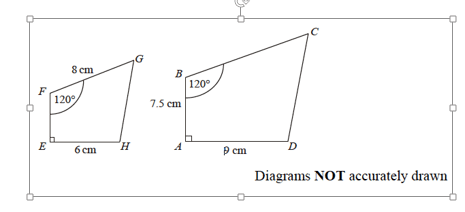
The scale factor is 1.5 (6 x 1.5 = 9, using EH and AD)

Length BC = 8 x 1.5 = 12cm

Length EF = 7.5 / 7 = 1.07cm

Areas and Volumes of Enlargements

For any pair of similar shapes,

• ratio of lengths = a : b
• ratio of areas = a² : b²
• ratio of volumes = a³ : b³

 

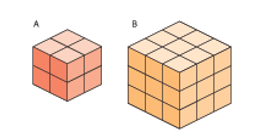
For this pair of cubes, A and B,

 

• ratio of lengths = 2 : 3
• ratio of areas = 2² : 3²=  4 : 9

• ratio of volumes = 2³ : 3³

                                            =  8 : 27

Example 1:

Two similar triangles have heights of 5cm and 45cm. Find the ratio of their surface areas and volumes.

 

• ratio of lengths = 5 : 7
• ratio of areas = 5² : 7²

= 25 : 49

Example 2:

Two similar pyramids have volumes of 64cm³ and 216cm³

ratio of volumes = 64 : 216

• To find the ratio of lengths, we need to work out the cubed roots of 64 and 216 as, remember ratio of volumes = a³: b³
• Ratio of volumes = 4³ : 6³
• Ratio of lengths = 4 : 6

Example 3:

 

Two triangles have a ratio of areas = 4 : 25

What is the length of a side on the smaller triangle when the length is 10cm on the larger triangle

• ratio of areas = 4 : 25

= 2² : 5²

• ratio of lengths = 2:5
• If the side on the larger triangle is 10cm, the side on the smaller triangle is 4cm

 Questions