Table of Contents
Unit 1 | Algebra
Page 1 | Expressions and Formulae
Page 3| Solving Linear Equations
Page 4| Expanding and Factorising
Page 5| Factorising Quadratics and expanding double brackets
Page 6| Patterns and Sequences
Page 7| Simultaneous Equations
Page 8| Changing the subject of a Formula
Page 9| Adding , subtracting algebraic formulas
Unit 2 |Graphs
Page 1 | Straight line graphs
Page 2 | Graphs of Quadratic functions
Unit 3 |Geometry and Measure
Page 2 | Symmetry
Page 3 | Coordinates
Page 4 | Perimeter, Area, Volume
Page 6 | Measurement
Page 7 | Trigonometry
Page 8 | Pythagoras
Page 9 | Angles
Page 10 | Shapes
Page 11| Time
Page 12 | Locus
Unit 4 | Numbers
Page 1 | Speed, Distance and time
Page 2 | Rounding and estimating
Page 3 | Ratio and proportion
Page 4 | Factors, Multiples and primes
Page 5 | Powers and roots
Page 7 | Positive and negative numbers
Page 8 | Basic operations
Page 9 | Fractions
Page 10 | Percentages
Unit 5 | Statistics and Probability
Page 1 | Sampling data (MA)
Page 2 | Recording and representing data
Page 3 | Mean median range and mode
Page 4 | Standard deviation
Unit 4 | Calculus
Geometry: Parallel Lines
L.O – To understand the properties of parallel lines and the rules of the angles they make
An extremely important point about parallel lines is that they never meet.
When parallel lines cross, there are rules regarding the angles that they make;
1.Vertically opposite angles are equal

Simply, two angles which are opposite eachother at a vertex, (corner) are equal.
2.Corresponding angles are equal
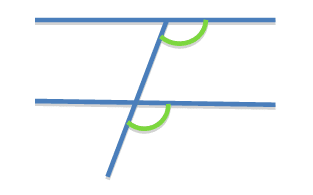
These angles are in a F shape
3.Alternate angles are equal
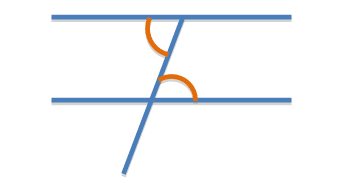
These angles are in a Z shape
4.Co interior angles add up to 180º

These angles are in a C shape
These angles are not equal, they add up to 180º
Examples:
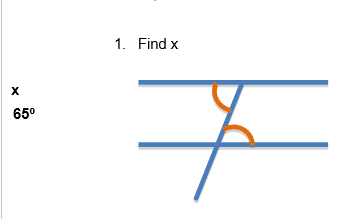
The first step is always to determine which type of angles you are looking at!
These angles are in a Z shape and hence are alternate angles
The rule about alternate angles is ‘alternate angles are equal’
Therefore, x = 65º
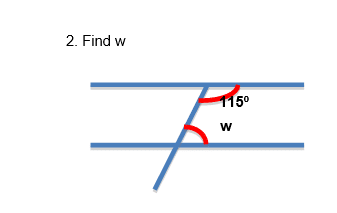
These angles are in a C shape and hence are co interior angles
The rule about co interior angles is ‘co interior angles add up to 180’
Therefore, w = 65º (180º-115º)
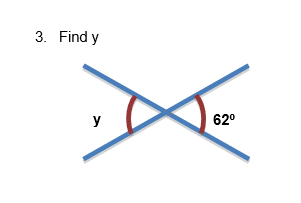
These angles are vertically opposite angles
The rule about vertically opposite angles is ‘vertically opposite angles are equal’
Therefore, y = 62º
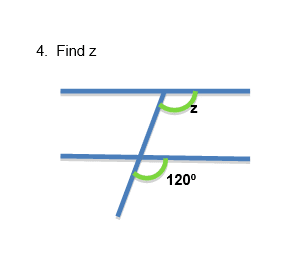
These angles are in a F shape and hence are corresponding angles
The rule about corresponding angles is ‘corresponding angles are equal
Therefore, z = 120º
More complex questions
Tips:
Here are a few tips to keep in mind when answering complex geometry questions.
- Find ALL the angles in whatever order you can
- Look out for the Z ,F and C shapes (don’t forget about vertically opposite angles aswell
- Remember to use the rules outlined above and also those under the ‘basic geometry section’. You may have to use several rules in order to find the angle in the question
- You may need to extend lines (make lines longer), in order to make the ‘letters’ (Z, F and C) more obvious
- Do not measure angles in geometry questions
- Don’t assume anything e.g. an angle may look like a right angle but unless it has the ‘box’ symbol, it isn’t one! Also, a triangle may look like an isosceles triangle but remember isosceles triangles have markings to indicate the two equal sides!
- Write all the angles you have found onto the diagram – this will help you to see which angles you can now find with this information
Example 1:
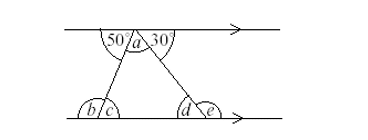
- Let’s start by finding angle a. Using the rule ‘angles on a straight line add up to 180º, a = 180º – 50º – 30º = 100º
- We can find angle c using the rule ‘alternate (Z) angles are equal’, c = 50º
- We can find angle b using the rule ‘co interior (C) angles add up to 180º, b= 180º – 50º = 130º
- We can find angle d using the basic rule ‘angles in a triangle add up to 180º’, d= 180º – a – c = 180º – 100º – 130º = 50º
- Finally, we can find angle e using the rule ‘co interior (C) angles add up to 180º
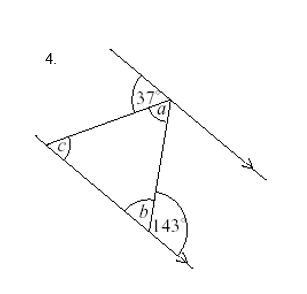
Example 2:
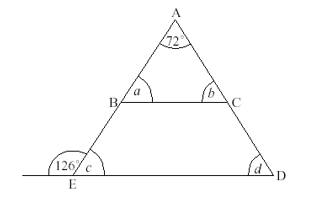
- Always start by finding the ‘easiest’ angles, you don’t have to work alphabetically, just work out whichever angle you can.
Angle c can be found using the rule ‘angles on a straight line add up to 180º’, c = 180º – 126º = 54º
- We can find angle a using the rule ‘corresponding angles (F) are equal’, a = 54º
- Angle b can then be found using the rule ‘angles in a triangle add up to 180º’, b = 180º – 72º – 54º = 54º
- Finally, angle d can be found using the rule ‘corresponding angles (F) angles are equal,’ d = 54º
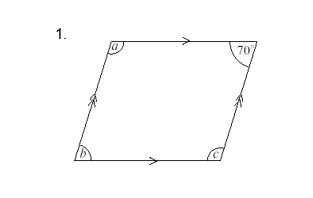
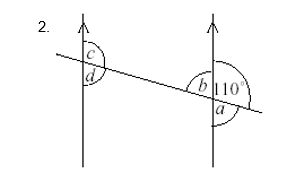
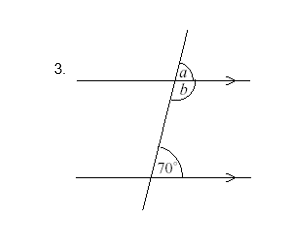
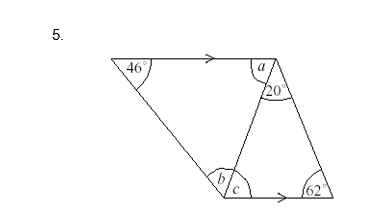
Questions:
Find the marked angles