Table of Contents
Unit 1 | Algebra
Page 1 | Expressions and Formulae
Page 3| Solving Linear Equations
Page 4| Expanding and Factorising
Page 5| Factorising Quadratics and expanding double brackets
Page 6| Patterns and Sequences
Page 7| Simultaneous Equations
Page 8| Changing the subject of a Formula
Page 9| Adding , subtracting algebraic formulas
Unit 2 |Graphs
Page 1 | Straight line graphs
Page 2 | Graphs of Quadratic functions
Unit 3 |Geometry and Measure
Page 2 | Symmetry
Page 3 | Coordinates
Page 4 | Perimeter, Area, Volume
Page 6 | Measurement
Page 7 | Trigonometry
Page 8 | Pythagoras
Page 9 | Angles
Page 10 | Shapes
Page 11| Time
Page 12 | Locus
Unit 4 | Numbers
Page 1 | Speed, Distance and time
Page 2 | Rounding and estimating
Page 3 | Ratio and proportion
Page 4 | Factors, Multiples and primes
Page 5 | Powers and roots
Page 7 | Positive and negative numbers
Page 8 | Basic operations
Page 9 | Fractions
Page 10 | Percentages
Unit 5 | Statistics and Probability
Page 1 | Sampling data (MA)
Page 2 | Recording and representing data
Page 3 | Mean median range and mode
Page 4 | Standard deviation
Unit 4 | Calculus
Polygons
L.O – To become familiar with the properties of regular polygons. Also be able to learn and use formulas associated with angles of polygons
A polygon = a shape with many sides.
A regular polygon = a shape where all the sides and the angles are the same
Here are the regular polygons you should be familiar with;
Equilateral Triangle:
3 sides
3 lines of symmetry
Rotational symmetry order 3

Square:
4 sides
4 lines of symmetry
Rotational symmetry order 4
Regular Pentagon:
5 sides
5 lines of symmetry
Rotational symmetry order 5
Regular Hexagon:
6 sides
6 lines of symmetry
Rotational symmetry order 6
Regular Heptagon:
7 sides
7 lines of symmetry
Rotational symmetry order 7

Regular Octagon:
8 sides
8 lines of symmetry
Rotational symmetry order 8
Also remember
- Nonagon (9 sides)
- decagon (10 sides)
Angles in Polygons:
Make sure you understand what an interior and exterior angle is
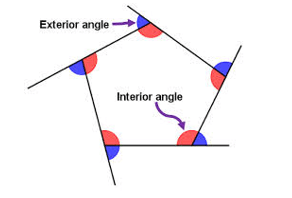

Here are the relevant formulas that need to be learnt!


As the examples show, you may need to use several formulas to work out an angle
Note – there may be more than one way to find the answer using these formulas. So if one way doesn’t work for you, try another formula/method!
Example 1:
Find the interior angle of a regular hexagon
- Using, Sum of Interior Angles = (n – 2) x 180°, where n = 6
= (6 – 2) x 180°
= 4 x180°
= 720°
- 720° is the sum of interior angles. We need to divide this by the number of sides to find the value of a single interior angle
720°/6 = 120°
- Interior angle = 120°
Example 2:
Calculate the exterior angle of a regular nonagon and hence, find the interior angle
- Sum of Exterior Angles = 360°
- To find the value of a single exterior angle, we need to divide 360° by the number of sides
360°/n = 40°
- Interior Angle = 180° – Exterior Angle
= 180° – 40°
= 140°
- Exterior Angle = 40° and Interior Angle = 140°

Example 3:
The interior angles of a regular polygon are each 120°. Calculate the number of sides
- The interior angles are 120° so the exterior angles = 180° – interior angles
= 180° – 120°
= 60°
- We know that exterior angle = 360°/n
n = 360°/exterior angle (by rearranging above formula)
n = 360°/ 60°
n = 6
– This regular polygon has 6 sides



