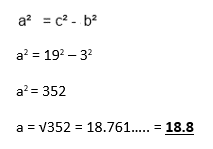Pythagoras’ Theorem

L.O To find the length of an unknown side using Pythagoras

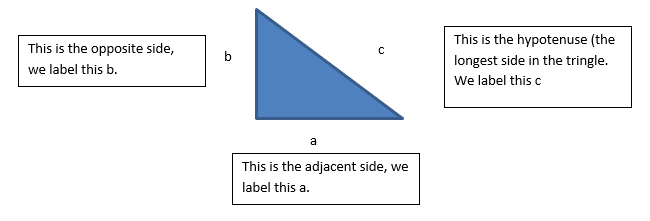
This is the method of finding the length of different sides in a right angled triangle.

Firstly, you should be comfortable with labelling the: adjacent, opposite and hypotenuse of any right angle triangle, we will cover this more on the Trigonometry section.

All you have to do is follow one simple rule:

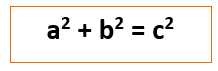
Let’s try an example:

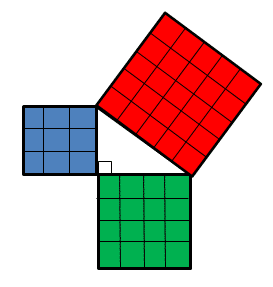
Here we have a right angle triangle with side lengths of 3cm,4cm and 5cm.

Pythagoras’ Theorem uses the square of the length of each side.

Now if we look at the areas of each square:

The area of the square on the side length of 3cm is 9cm

The area of the square on the side length of 4cm is 16cm

The area of the square on the side length of 5cm (the hypotenuse)  is 25cm

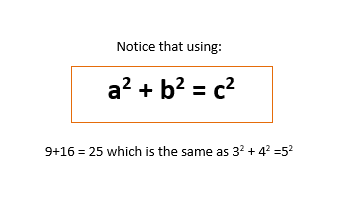
Example 1:

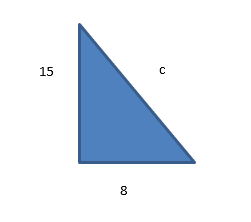
Work out the length of the hypotenuse of this triangle

Always state Pythagoras’ Theorem first

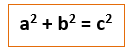
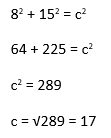
Example 2:

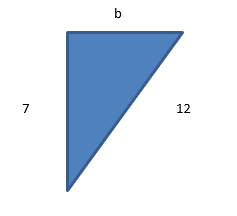
Work out the length of the Opposite side of this triangle to 3 s.f

Now we have to rearrange Pythagoras’ Theorem

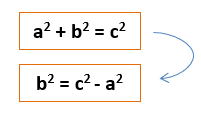
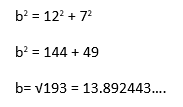
However the question asks the answer to 3 significant figures so make sure your answer is 13.9

Example 3:

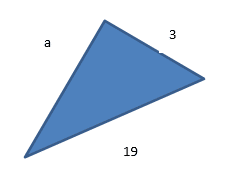
Work out the length of the adjacent side to 3 s.f.

Step 1: Rearrange in the same way as you did in the example above but this time subtract b².