Table of Contents
Unit 1 | Algebra
Page 1 | Expressions and Formulae
Page 3| Solving Linear Equations
Page 4| Expanding and Factorising
Page 5| Factorising Quadratics and expanding double brackets
Page 6| Patterns and Sequences
Page 7| Simultaneous Equations
Page 8| Changing the subject of a Formula
Page 9| Adding , subtracting algebraic formulas
Unit 2 |Graphs
Page 1 | Straight line graphs
Page 2 | Graphs of Quadratic functions
Unit 3 |Geometry and Measure
Page 2 | Symmetry
Page 3 | Coordinates
Page 4 | Perimeter, Area, Volume
Page 6 | Measurement
Page 7 | Trigonometry
Page 8 | Pythagoras
Page 9 | Angles
Page 10 | Shapes
Page 11| Time
Page 12 | Locus
Unit 4 | Numbers
Page 1 | Speed, Distance and time
Page 2 | Rounding and estimating
Page 3 | Ratio and proportion
Page 4 | Factors, Multiples and primes
Page 5 | Powers and roots
Page 7 | Positive and negative numbers
Page 8 | Basic operations
Page 9 | Fractions
Page 10 | Percentages
Unit 5 | Statistics and Probability
Page 1 | Sampling data (MA)
Page 2 | Recording and representing data
Page 3 | Mean median range and mode
Page 4 | Standard deviation
Unit 4 | Calculus
Solving Linear Equations with Fractions
L.O To be able to interpret fractional equations and solve them using the inverse method
In algebraic expressions whenever a term is divided by another, fractions instead of division signs are used to represent this.


Example 1:
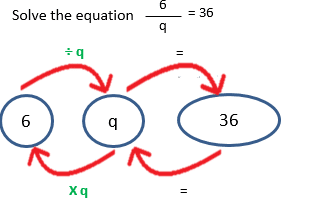
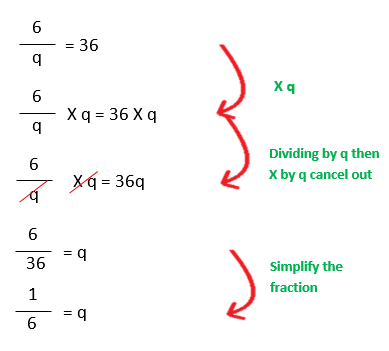



Example 2 :
![]()
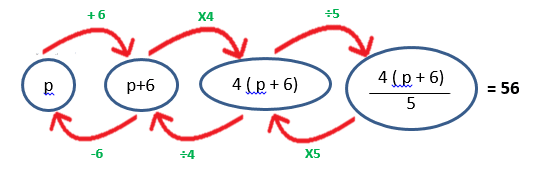
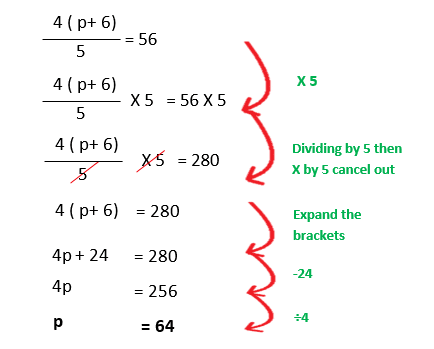



Example 3 :
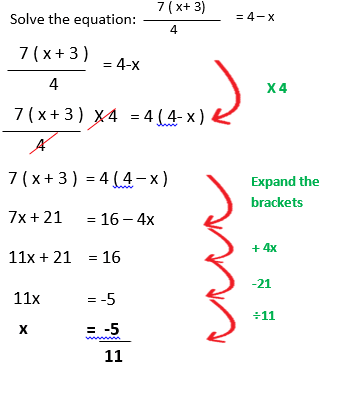



Example 4:

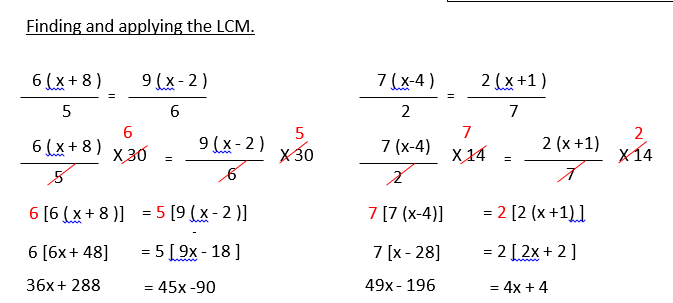





Word Problems
a) Amara thinks of a number. She adds 3 and then divides it by 2 to receive an answer. Abdul on the other hand starts with a number, subtracts 5 and then divides by 3. When they reveal their numbers they notice they started with the same number initially. Write down expressions for both Amara and Abdul and work out the number they started with.



b) Ibrahim drives Rickshaw’s in India. On one journey he travels for ¾ of an hour at the speed of p km per hour. He then travels for 1/5 of an hour at the speed of (p + 5) km per hour. When he looks at his mileage it appears he has done 30 miles. Work out the value of p.




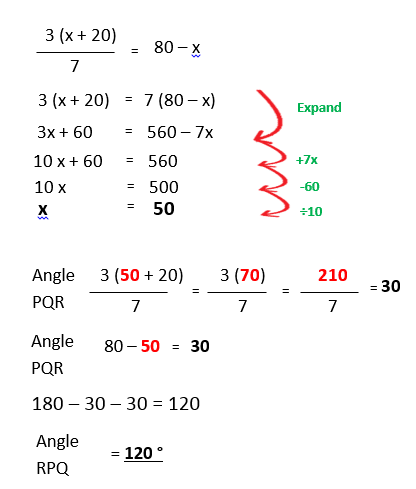
c) Alina has an Isosceles triangle. The length of the sides PQ and PR are the same. The angle PQR is 3/7(x+20) and PRQ is 80 – x. Using this information find x and then the size of the remaining angle.