Multiplying and Dividing by 10, 100 and 1000

1. Once you get the hang of it, multiplying and dividing by 10, 100 and 1000. All it involves is moving every digit either to the right or the left. It’s important that you remember how place value works though.

2. We’ll start with multiplication. When you multiply a number by 10, 100, or 1000, it’s getting bigger so all of the digits will have to move to the left.

3. You look at the number of zeros in what you’re multiplying to tell you how many spaces you need to move – when you’re multiplying by 100, it has two zeroes so you have to move two spaces to the left (by 10, its one space and by 1000, its three spaces).

Example 1:

Let’s say this is the question we have -> 263 x 100

We’re multiplying by 100 so this means that we’re going to be moving 2 spaces to the left. Let’s set this out in a place value chart.

There was nothing left in the tens and the units columns so we had to put a zero in there. Our answer is 26 300.

4.  Dividing by 10, 100 or 1000 is very similar to multiplying but this time, all the digits in the place value chart will be moving to the right, because they’re getting smaller.

5. Like with multiplication, the number of zeros in what you’re dividing by tells you how many spaces you need to move – dividing by 10 is one space to the right, by 100 is two and by 1000 is three.

Example 2:

Let’s say our next question is 840 ÷ 1000

We’re dividing by 1000 so that means we have to move 3 spaces to the right. We’ll use the place value chart to do this again.

Our answer is 0.840 but we can just write this as 0.84.

6. These methods of multiplying and dividing can be useful even when your question has multiples of 10 or 100 or 1000. You just have to break up the question – for example if you have 25 x 30, you can change this to 25 x 3 x 10. You can find out that 25 x 3 is 75 the you just have to multiply 75 x 10.

7. Similarly, you can break up division questions. If you had 360 ÷ 40 , we know that 40 is the same as 4 x 10 so we can do 360 ÷ 4, which is 90, then divide that by 10.

1) Complete the questions

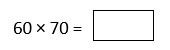
2) What number is 10 times larger than 7.1?

3) How many times smaller is 39 than 3900?

4) Each many question will he have constructed in 100 days?

How many question will he have constructed n 100 days?

5) Johns grandfather splits a 2.5kg bag of flour into 10 containers.

6) A schools is holding a harvest fund raiser. Each child has asked to bling in
15 different item sot food.

There are 125 children in the school.

How much food will there be in total?