Table of Contents
Unit 1 | Algebra
Page 1 | Expressions and Formulae
Page 3| Solving Linear Equations
Page 4| Expanding and Factorising
Page 5| Factorising Quadratics and expanding double brackets
Page 6| Patterns and Sequences
Page 7| Simultaneous Equations
Page 8| Changing the subject of a Formula
Page 9| Adding , subtracting algebraic formulas
Unit 2 |Graphs
Page 1 | Straight line graphs
Page 2 | Graphs of Quadratic functions
Unit 3 |Geometry and Measure
Page 2 | Symmetry
Page 3 | Coordinates
Page 4 | Perimeter, Area, Volume
Page 6 | Measurement
Page 7 | Trigonometry
Page 8 | Pythagoras
Page 9 | Angles
Page 10 | Shapes
Page 11| Time
Page 12 | Locus
Unit 4 | Numbers
Page 1 | Speed, Distance and time
Page 2 | Rounding and estimating
Page 3 | Ratio and proportion
Page 4 | Factors, Multiples and primes
Page 5 | Powers and roots
Page 7 | Positive and negative numbers
Page 8 | Basic operations
Page 9 | Fractions
Page 10 | Percentages
Unit 5 | Statistics and Probability
Page 1 | Sampling data (MA)
Page 2 | Recording and representing data
Page 3 | Mean median range and mode
Page 4 | Standard deviation
Unit 4 | Calculus
Symmetry in 2D Shapes
Symmetry is show when you can draw a line through a shape and the shapes created on either side of the line would be exactly the same but reflected (flipped over). This line would be called a line of symmetry. A shape can have one line of symmetry, several lines of symmetry or no lines of symmetry whatsoever.
Let’s see if we can find lines of symmetry in some common 2D shapes.
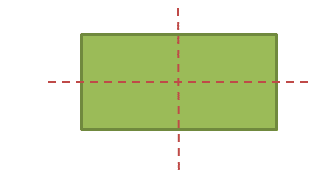
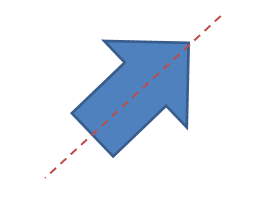
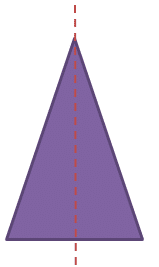


Regular polygons will have the number of lines of symmetry as they have sides. A square will have 4 lines of symmetry, a pentagon will have 5, and a hexagon will have 6 and so on.
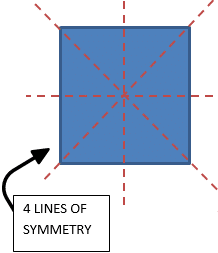
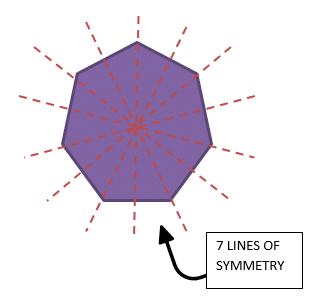
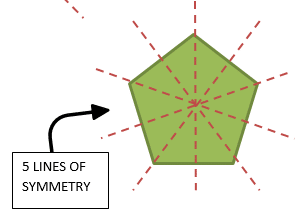
Symmetry in 2D Shapes Exercise

 1) Draw all of the lines of symmetry into the following shapes
1) Draw all of the lines of symmetry into the following shapes
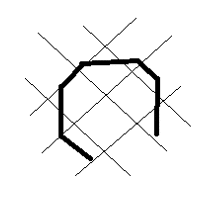
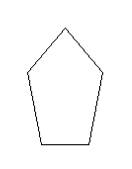
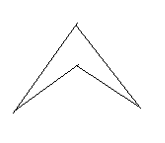
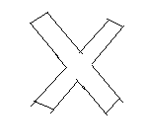
[bg_collapse view=”link” color=”#fafafa” expand_text=”Reveal Answer” collapse_text=”Hide Answer” inline_css=”background: #2ea3f2; padding: 9px; font-size: 14px; font-weight: 600;” ][/bg_collapse]
 2) Using the straight line as a line of symmetry, complete the pattern.
2) Using the straight line as a line of symmetry, complete the pattern.
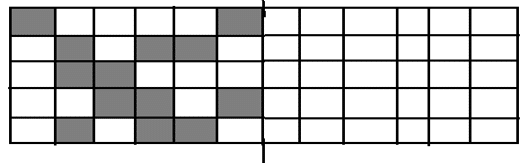
[bg_collapse view=”link” color=”#fafafa” expand_text=”Reveal Answer” collapse_text=”Hide Answer” inline_css=”background: #2ea3f2; padding: 9px; font-size: 14px; font-weight: 600;” ][/bg_collapse]
 3) Which of the following shapes have reflective symmetry?
3) Which of the following shapes have reflective symmetry?

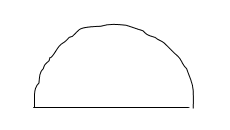
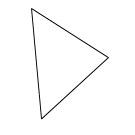
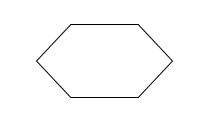
[bg_collapse view=”link” color=”#fafafa” expand_text=”Reveal Answer” collapse_text=”Hide Answer” inline_css=”background: #2ea3f2; padding: 9px; font-size: 14px; font-weight: 600;” ][/bg_collapse]
 4) Complete the shape, using the black line that these is reflective symmetry.
4) Complete the shape, using the black line that these is reflective symmetry.
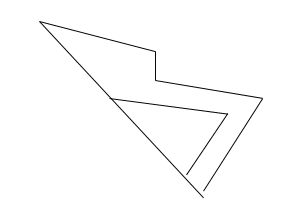
[bg_collapse view=”link” color=”#fafafa” expand_text=”Reveal Answer” collapse_text=”Hide Answer” inline_css=”background: #2ea3f2; padding: 9px; font-size: 14px; font-weight: 600;” ][/bg_collapse]
 5) The following shape is made up of four squares
5) The following shape is made up of four squares

Add four more of those squares to give the shape ONLY one line of symmetry.
[bg_collapse view=”link” color=”#fafafa” expand_text=”Reveal Answer” collapse_text=”Hide Answer” inline_css=”background: #2ea3f2; padding: 9px; font-size: 14px; font-weight: 600;” ][/bg_collapse]

