Table of Contents
Algebra | Unit 1 | Expressions and Formula
Page 3| Changing the Subject of a Formula
Algebra | Unit 2 | Inequalities
Page 1 | Number Lines
Page 2 | Solving Inequalities
Algebra | Unit 3 | Equations
Page 2 | Equations with Brackets
Page 3 | Equations with Fractions
Algebra | Unit 4 | Graphs
Page 1 | Straight Line Graphs ( y = mx + c )
Algebra | Unit 5 | Patterns and Sequences
Page 1 | Basic Patterns
Page 2 | Linear Sequences & nth term
Page 3 | Quadratic Equations
Shape, Space and Measure | Unit 1 |Transformations
Page 1 | Congruent Shapes
Page 2 | Translations
Page 3 | Rotations
Page 4 | Reflections
Page 5 | Enlargements
Shape, Space and Measure | Unit 2 |Symmetry
Page 1 | Line Symmetry
Page 2 | Rotational Symmetry
Shape, Space and Measure | Unit 2 |Coordinates
Page 1 | Plotting Coordinates
Shape, Space and Measure | Unit 3 |Perimeter, Area, Volume
Shape, Space and Measure | Unit 4 |Measurement
Page 1 | Estimation and Accuracy
Page 2 | Scales
Page 3 | Conversions (Metric & Imperial)
Page 4 | Area and Volume Unit Conversions
Shape, Space and Measure | Unit 5 |Trigonometry
Page 1 | Triangle Construction
Shape, Space and Measure | Unit 6 |Pythagoras
Page 1 | Pythagoras Theorem
Page 2 | Line Segments
Shape, Space and Measure | Unit 7 |Angles
Page 1 | Summary of Drawing &Reading Angles
Page 2 | Angle Sum in Different Shapes
Page 3 | Angles in a Polygon
Page 4 | Angles and Parallel Lines
Page 5 | Perpendicular Bisectors
Page 6 | Angle Bisectors
Page 7 | Constructing Loci
Shape, Space and Measure | Unit 8 |Shapes
Page 1 | Properties of Circles
Page 2 | Properties of Polygons
Page 3 | Properties of Triangles
Page 4 | 3D Shapes: Nets & Faces
Shape, Space and Measure | Unit 8 |Time
Page 1 | Units of Time
Page 2 | 12 & 24 Hour Clocks
Page 3 | Timetables
Number | Unit 1 |Place Value
Number | Unit 2 |Distance, Speed and Time
Number | Unit 3 |Rounding and estimating
Number | Unit 4 |Ratio and Proportion
Page 1 | Equivalent Ratios
Page 2 | Division with Ratios
Page 3 | Scale Drawings & Maps
Page 4 | Proportions
Number | Unit 5 |Primer numbers, factors and multiples
Number | Unit 6 |Powers and roots
Number | Unit 7 |Decimals
Page 1 | X 10, 100 & 1000
Page 2 | ÷10, 100 & 1000
Page 3 | Multiplying and Dividing by Whole Numbers
Number | Unit 8 |Positive and negative numbers
Page 1 | Operations with Positive and Negative Numbers
Number | Unit 9 |Operations
Page 1 | BIDMAS Rule
Page 2 | Multiplication & Division (Different Methods)
Page 3 | Converting Fractions, Decimals & Percentages
Number | Unit 10 |Fractions
Page 1 | Equivalent Fractions
Page 2 | Simplifying Fractions
Page 3 | Mixed Numbers
Page 4 | Improper Fractions
Page 5 | Ordering Fractions
Page 6 | Addition & Subtraction
Page 7 | Multiplication & Division
Number | Unit 11 |Percentages
Page 1 | Percentages of Quantities
Page 2 | Interest, Wages & Quantities
Number | Unit 12 |Standard Index form
Page 1 | Decimals in Standard Form
Page 2 | Writing in Standard Form
Page 3 | Addition and Subtraction un Standard Form
Page 4 | Multiplication and Division in Standard Form
Handling Data | Unit 1 |Collecting & Recording Data Representing Data
Page 1 | Tables & Tally Diagrams
Page 2 | Frequency Tables
Page 3 | Stem & Leaf Diagrams
Handling Data | Unit 2 |Representing Data
Page 1 | Bar Charts
Page 2 | Line Graphs
Page 3 | Pictograms
Page 4 | Frequency Polygons
Page 5 | Scatter Diagrams
Page 6 | Pie Charts
Handling Data | Unit 2 |Averages
Page 1 | Mean, Median, Mode & Range
Page 2 | Averages of Grouped Data
Handling Data | Unit 2 |Probability
Page 1 | Basic Probability
Page 2 | Sum of Probabilities
Page 3 | Probability of Combined Events
Solving Equations
L.O to be able to find the solution to double barrel equations involving multiple terms in the equation
Solving equations is the same as solving formula but equations can be more complex in the sense that there can be the same term on both sides. For instance some equations can take the form of:
![]()
This makes it more complex when solving the equation and finding the exact value of x.
The way to tackle equations like these is to get all the X’s on the same side. Thereafter applying the inverses will allow you to find the exact value of x.
For instance with the equation:
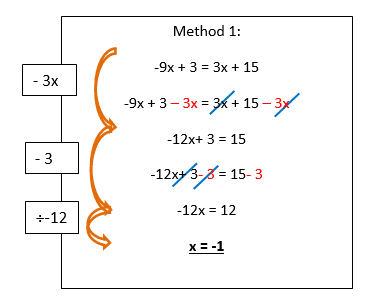
4x + 6 = 2x + 8
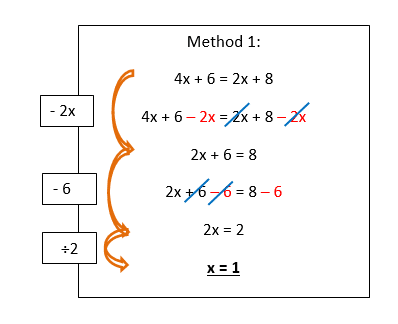
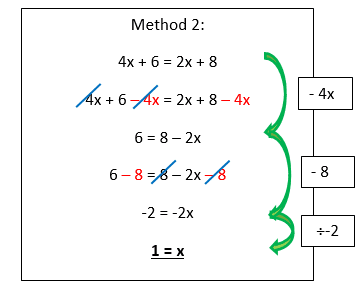
Note how both methods give you the same solution. This is because both methods start by placing the x terms on the same side. This can either be done by –2xwhich would cancel out the x terms on the LHS as method 1 shows. However the same can be done by -4xwhich would cancel out the x terms on the RHS as method 2 suggests.
The latter steps are ones you should now be familiar with from solving formulae and inequalities: these steps simply involve applying the inverse operations.
Example 1: Solve the following equation 6x – 7 = 2x + 9
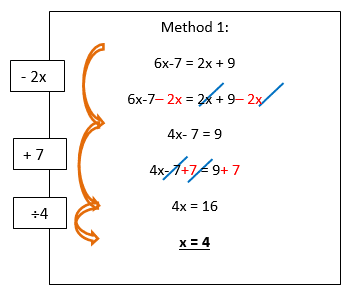



Example 2 : Solve the following equation -9x + 3 = 3x + 15