Table of Contents
Algebra | Unit 1 | Expressions and Formula
Page 3| Changing the Subject of a Formula
Algebra | Unit 2 | Inequalities
Page 1 | Number Lines
Page 2 | Solving Inequalities
Algebra | Unit 3 | Equations
Page 2 | Equations with Brackets
Page 3 | Equations with Fractions
Algebra | Unit 4 | Graphs
Page 1 | Straight Line Graphs ( y = mx + c )
Algebra | Unit 5 | Patterns and Sequences
Page 1 | Basic Patterns
Page 2 | Linear Sequences & nth term
Page 3 | Quadratic Equations
Shape, Space and Measure | Unit 1 |Transformations
Page 1 | Congruent Shapes
Page 2 | Translations
Page 3 | Rotations
Page 4 | Reflections
Page 5 | Enlargements
Shape, Space and Measure | Unit 2 |Symmetry
Page 1 | Line Symmetry
Page 2 | Rotational Symmetry
Shape, Space and Measure | Unit 2 |Coordinates
Page 1 | Plotting Coordinates
Shape, Space and Measure | Unit 3 |Perimeter, Area, Volume
Shape, Space and Measure | Unit 4 |Measurement
Page 1 | Estimation and Accuracy
Page 2 | Scales
Page 3 | Conversions (Metric & Imperial)
Page 4 | Area and Volume Unit Conversions
Shape, Space and Measure | Unit 5 |Trigonometry
Page 1 | Triangle Construction
Shape, Space and Measure | Unit 6 |Pythagoras
Page 1 | Pythagoras Theorem
Page 2 | Line Segments
Shape, Space and Measure | Unit 7 |Angles
Page 1 | Summary of Drawing &Reading Angles
Page 2 | Angle Sum in Different Shapes
Page 3 | Angles in a Polygon
Page 4 | Angles and Parallel Lines
Page 5 | Perpendicular Bisectors
Page 6 | Angle Bisectors
Page 7 | Constructing Loci
Shape, Space and Measure | Unit 8 |Shapes
Page 1 | Properties of Circles
Page 2 | Properties of Polygons
Page 3 | Properties of Triangles
Page 4 | 3D Shapes: Nets & Faces
Shape, Space and Measure | Unit 8 |Time
Page 1 | Units of Time
Page 2 | 12 & 24 Hour Clocks
Page 3 | Timetables
Number | Unit 1 |Place Value
Number | Unit 2 |Distance, Speed and Time
Number | Unit 3 |Rounding and estimating
Number | Unit 4 |Ratio and Proportion
Page 1 | Equivalent Ratios
Page 2 | Division with Ratios
Page 3 | Scale Drawings & Maps
Page 4 | Proportions
Number | Unit 5 |Primer numbers, factors and multiples
Number | Unit 6 |Powers and roots
Number | Unit 7 |Decimals
Page 1 | X 10, 100 & 1000
Page 2 | ÷10, 100 & 1000
Page 3 | Multiplying and Dividing by Whole Numbers
Number | Unit 8 |Positive and negative numbers
Page 1 | Operations with Positive and Negative Numbers
Number | Unit 9 |Operations
Page 1 | BIDMAS Rule
Page 2 | Multiplication & Division (Different Methods)
Page 3 | Converting Fractions, Decimals & Percentages
Number | Unit 10 |Fractions
Page 1 | Equivalent Fractions
Page 2 | Simplifying Fractions
Page 3 | Mixed Numbers
Page 4 | Improper Fractions
Page 5 | Ordering Fractions
Page 6 | Addition & Subtraction
Page 7 | Multiplication & Division
Number | Unit 11 |Percentages
Page 1 | Percentages of Quantities
Page 2 | Interest, Wages & Quantities
Number | Unit 12 |Standard Index form
Page 1 | Decimals in Standard Form
Page 2 | Writing in Standard Form
Page 3 | Addition and Subtraction un Standard Form
Page 4 | Multiplication and Division in Standard Form
Handling Data | Unit 1 |Collecting & Recording Data Representing Data
Page 1 | Tables & Tally Diagrams
Page 2 | Frequency Tables
Page 3 | Stem & Leaf Diagrams
Handling Data | Unit 2 |Representing Data
Page 1 | Bar Charts
Page 2 | Line Graphs
Page 3 | Pictograms
Page 4 | Frequency Polygons
Page 5 | Scatter Diagrams
Page 6 | Pie Charts
Handling Data | Unit 2 |Averages
Page 1 | Mean, Median, Mode & Range
Page 2 | Averages of Grouped Data
Handling Data | Unit 2 |Probability
Page 1 | Basic Probability
Page 2 | Sum of Probabilities
Page 3 | Probability of Combined Events
Writing Formula
L.O to be able to write and understand algebraic formulae for word problems
Formulae are a way of rewriting problems or describing a rule. They are written in algebraic form which means that letters are used. However the main element that shows that something is a formulae is that it will contain an = sign. Without even thinking about it, you have already been using formulae in maths before; for instance when working out the area of a triangle.
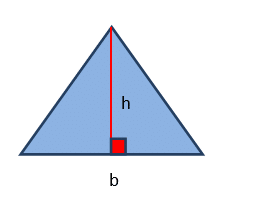
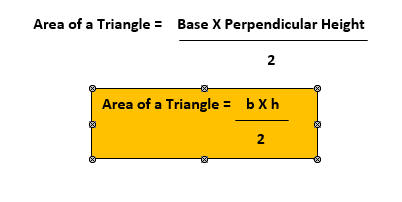
Here the base and perpendicular heighthave been abbreviated, shortened, to b and h. This is exactly the point of formulas, to make solving problems later on easier, in such a way that any measurement can be applied to the formulae. Similarly you have already used formulas when working out other problems (notably areas) for example:
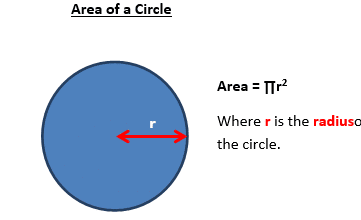
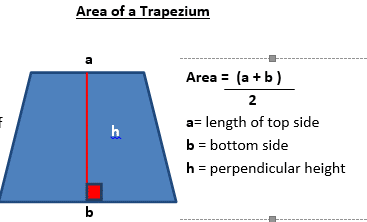
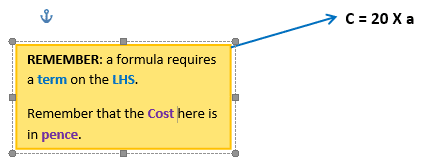
Note how each of these formulas have an = sign. Now you are familiar with what formulas look like, it is now time to substitute values into formula As shown above, formulae can be used to help solve problems. However you need to be able to write formulae before you can solve or manipulate them further. For instance if in a supermarket you see an apple for 20p and you wanted to buy 3 apples, you would mentally apply the following calculation: 1 apple is 20p 2 apples are (20 X 2) = 40p 3 apples are (20 X 3) = 60p So the formula to work out the cost of buying a number of apples is:
Cost= 20 x number of apples being bought


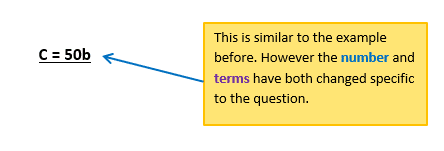
Cake baskets are £50 each. Samantha has many friends coming and wants a formula to help calculate the cost. In this example you would do as before: 1 basket = £50 2 baskets are (50 X 2) = £100 3 baskets are (50 X 3) = £150
Cost = 50 x number of basket being bought

Example 1: Jane is going to order some parcels online. Each parcel costs £5 but also has a small administration fee of £2.50 for each order processed. Write a formula to calculate the cost of one of Jane’s orders.




Example 2: Aqif is having a banquet. The cost of a 3 course meal per adults is £15, per child is £6 and for younger children is £3. There is also a fee of £35 for hiring the hall. Write a formula to calculate the cost of Aqif’s banquet.





Example 3: A group of 6 friends are making a fruit basket containing: apples at 60p each, pears at 40p and oranges at 80p each. They decide to split the cost of the basket equally between them. Write a formula for the cost of each person.



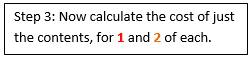


Example 4: Sarah is having a birthday party and wants to make 5 bags that contain a different number of toys (30p), sweets (50p) and messages (55p). Write a formula for a given number of items for 5 party bags.






