Table of Contents
Unit 1 | Algebra
Page 1 | Expressions and Formulae
Page 3| Solving Linear Equations
Page 4| Expanding and Factorising
Page 5| Factorising Quadratics and expanding double brackets
Page 6| Patterns and Sequences
Page 7| Simultaneous Equations
Page 8| Changing the subject of a Formula
Page 9| Adding , subtracting algebraic formulas
Unit 2 |Graphs
Page 1 | Straight line graphs
Page 2 | Graphs of Quadratic functions
Unit 3 |Geometry and Measure
Page 2 | Symmetry
Page 3 | Coordinates
Page 4 | Perimeter, Area, Volume
Page 6 | Measurement
Page 7 | Trigonometry
Page 8 | Pythagoras
Page 9 | Angles
Page 10 | Shapes
Page 11| Time
Page 12 | Locus
Unit 4 | Numbers
Page 1 | Speed, Distance and time
Page 2 | Rounding and estimating
Page 3 | Ratio and proportion
Page 4 | Factors, Multiples and primes
Page 5 | Powers and roots
Page 7 | Positive and negative numbers
Page 8 | Basic operations
Page 9 | Fractions
Page 10 | Percentages
Unit 5 | Statistics and Probability
Page 1 | Sampling data (MA)
Page 2 | Recording and representing data
Page 3 | Mean median range and mode
Page 4 | Standard deviation
Unit 4 | Calculus
Equivalent Fractions
- Fractions represent a portion of the whole. Different fractions which represent an equal amount of the whole are called equivalent fractions.
- In order to find different equivalent fractions, we can multiply or divide both the numerator and denominator of the fractions we already have.
- For example, if we wanted to find an equivalent fraction of
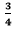 , we could do this multiplying both numbers by two, which would give us
, we could do this multiplying both numbers by two, which would give us 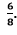 .
.
Example 1 :
Take a look at this cake. We can cut it into different numbers of slices and still represent one half.
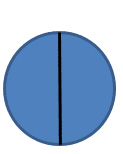
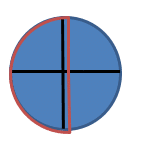
In the first circle, we can show a half by taking one piece out of a possible two, so this is ![]()
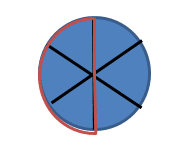
In the second circle, one half is shown by highlighting 2 pieces out of a possible four, so this is ![]()
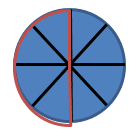
The third circle is ![]() and the fourth circle is
and the fourth circle is ![]() .
.
As all of these fractions represent the same amount of space, we would say that they are equivalent fractions. We can see that the numerator and denominator of the first fraction ![]() have been multiplied by 2, 3 and 4 to get the other fractions.
have been multiplied by 2, 3 and 4 to get the other fractions.
4. Equivalent fractions can come in very useful when we need to compare fractions that have different denominators.
5.If we can use equivalent fractions to make both fractions have the same denominator, all we have to do is compare the numerator.
Example 2 :
Let’s say that we need to find out whether ![]() or is larger
or is larger ![]() .
.
- First, we need to find a number that both of the denominators are factors of (they fit into it a specific number of times). 8 and 12 both fit into 24 so we’ll choose that as our new denominator. 7
- Secondly, we need to find out what we need to multiply each fraction by so that it has a denominator of 24 – whatever we’ve done to each of our denominators has to also be done to the numerator.
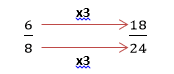
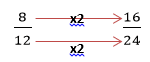
- If we compare the two fractions, we can now clearly see that 6/8 must be bigger than 8/12, as the numerator is bigger when it is converted.
6. If you can see that the numerator and the denominator both have the same factor, you can divide them both by this factor, which is called cancelling.
7. Once a fraction cannot be cancelled anymore, it is said to be in its simplest form.
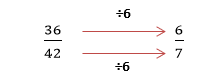
Example 3 :
The fraction we can use for our example is ![]()
Both 36 and 42 are in the 6 times table, so we can cancel by a factor of six.