Circle Geometry

---

L.O – To be able to recognise and apply the rules of circle geometry

Don’t worry too much about the explanations in blue – they can be a bit confusing!

Make sure you memorise all the rules and be able to recognise the rules when you see the images as shown below

1. Angle in a semicircle = 90º

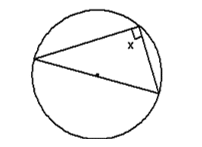
x = 90º
A triangle where the base is the diameter of the circle will always make an angle of 90º, where the triangle hits the edge of the circle.

(The angle we are referring too is the one opposite the diameter/not in contact with the diameter of the circle)

 

2. Angle at the centre is double the angle at the edge

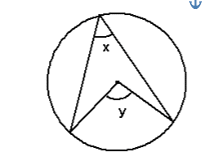
y = 2x

The angle subtended (made) at the centre of a circle is double the angle at the edge from the same two points.

3. Angles in the same segment are equal

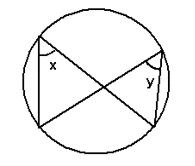
x = y

Angles subtended (made) by the same arc at the circumference are equal

4. Opposite angles of a cyclic quadrilateral add up to 180º

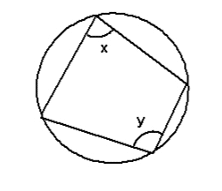
x + y = 180º

A cyclic quadrilateral is a 4 sided shapes formed inside a circle, with all 4 vertices touching the circumference of the circle

 

5.The angle between a tangent and radius is 90º

A tangent to a circle is a line which touches the circle at one point

A tangent is always at right angles to the radius at the point it touches the circles

 

6. Chord bisector is a diameter

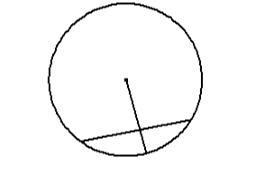
A chord is any line drawn across a circle

The line that cuts the chord in half (bisects it), is the diameter of the circle as it goes through the centre of the circle.

7. Alternate segment theorem

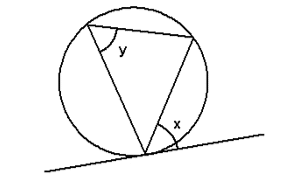
The angle between the tangent and chord at the point of contact is equal to the angle in the alternate segment.

8. Tangents from a point outside the circle are equal in length

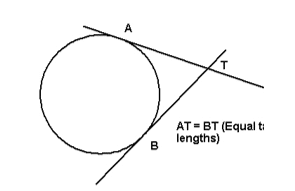
Two tangents to a circle from a point (T) are equal

Example 1:

Find angle BAC

Angle ACB = 90º

   Angle in a semicircle = 90º

Angle BAC = 35º

   Angles in a triangle add up to 180º

 

Find angle POQ

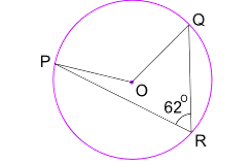
Angle POQ= 124º

   Angle at the centre is double the angle at the edge

 

Find angle CBX

Angle  ACB = 32º

   Angles in the same segment are equal

 

Angle CBX = 63º

   Angles in a triangle add up to 180º

Find angle WXY

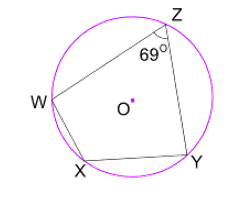
Angle WXY  = 111º

   Opposite angles in a cyclic quadrilateral add up to 180º

Find angle SRT

 

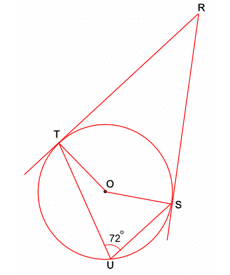
Angle SOT = 144º

   Angle at the centre is twice angle at circumference

Angle RSO and RTO = 90º

   Angle between a tangent and radius is 90º

Angle SRT = 36º

   Angles in a quadrilateral add up to 360º

Tips

• Always show your working and write out the rules you are using, especially in the exam!

 

• You may have to use several rules in order to find some angles!