Table of Contents
Unit 1 | Algebra
Page 1 | Expressions and Formulae
Page 3| Solving Linear Equations
Page 4| Expanding and Factorising
Page 5| Factorising Quadratics and expanding double brackets
Page 6| Patterns and Sequences
Page 7| Simultaneous Equations
Page 8| Changing the subject of a Formula
Page 9| Adding , subtracting algebraic formulas
Unit 2 |Graphs
Page 1 | Straight line graphs
Page 2 | Graphs of Quadratic functions
Unit 3 |Geometry and Measure
Page 2 | Symmetry
Page 3 | Coordinates
Page 4 | Perimeter, Area, Volume
Page 6 | Measurement
Page 7 | Trigonometry
Page 8 | Pythagoras
Page 9 | Angles
Page 10 | Shapes
Page 11| Time
Page 12 | Locus
Unit 4 | Numbers
Page 1 | Speed, Distance and time
Page 2 | Rounding and estimating
Page 3 | Ratio and proportion
Page 4 | Factors, Multiples and primes
Page 5 | Powers and roots
Page 7 | Positive and negative numbers
Page 8 | Basic operations
Page 9 | Fractions
Page 10 | Percentages
Unit 5 | Statistics and Probability
Page 1 | Sampling data (MA)
Page 2 | Recording and representing data
Page 3 | Mean median range and mode
Page 4 | Standard deviation
Unit 4 | Calculus
Ratio and proportion
- Ratios are way to express the size of one part in comparison to other parts.
- Proportions express the size of one part in comparison to the whole.
Example 1:
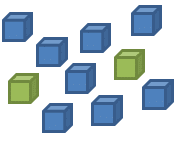
In this box of Lego bricks, there are 2 green bricks and 8 blue bricks. This means that for every one green brick, there are four blue bricks. We can write this as a ratio of 1:4.
If we want to write the number of green bricks as a proportion, it is 2/10, which can be simplified to 1/5.
3. If you want to multiply something that has ratios, it is important to remember that whatever is done to one of the parts must be done to all of the other parts.
Example 2:
A recipe for sponge cake has 100g flour, 2 eggs and 75g of sugar. As a ratio, we can write this as 100:2:75
Let’s say that we need to find out how much sugar we would need in a cake of the same ratios but with 300g of flour. The amount of flour has been tripled, so the other two parts must also be tripled.
75 x 3 = 225 – the new cake would need 225g of sugar.
1)
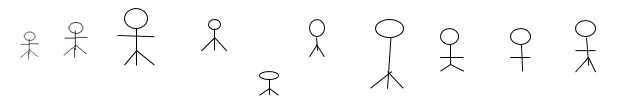

![]()
2) There are 30 children in a class.For every 2 boys there are 3 girls.
How many girls are there![]()
3) To make pancakes of for 8 people you need.
300g plan flour
6 large eggs
900ml milk
3 table spoon sunflower
How many eggs will be needed to serve 16 people.
4) In Toby’s class, There are 3 people with a cat for every person who has a dog.There are 24 people in his class.How many dogs are there?
5)
a) In this shape, How many triangle are there to squares?
b)What is the proportion of squares in the whole shape?