Table of Contents
Unit 1 | Algebra
Page 1 | Expressions and Formulae
Page 3| Solving Linear Equations
Page 4| Expanding and Factorising
Page 5| Factorising Quadratics and expanding double brackets
Page 6| Patterns and Sequences
Page 7| Simultaneous Equations
Page 8| Changing the subject of a Formula
Page 9| Adding , subtracting algebraic formulas
Unit 2 |Graphs
Page 1 | Straight line graphs
Page 2 | Graphs of Quadratic functions
Unit 3 |Geometry and Measure
Page 2 | Symmetry
Page 3 | Coordinates
Page 4 | Perimeter, Area, Volume
Page 6 | Measurement
Page 7 | Trigonometry
Page 8 | Pythagoras
Page 9 | Angles
Page 10 | Shapes
Page 11| Time
Page 12 | Locus
Unit 4 | Numbers
Page 1 | Speed, Distance and time
Page 2 | Rounding and estimating
Page 3 | Ratio and proportion
Page 4 | Factors, Multiples and primes
Page 5 | Powers and roots
Page 7 | Positive and negative numbers
Page 8 | Basic operations
Page 9 | Fractions
Page 10 | Percentages
Unit 5 | Statistics and Probability
Page 1 | Sampling data (MA)
Page 2 | Recording and representing data
Page 3 | Mean median range and mode
Page 4 | Standard deviation
Unit 4 | Calculus
Changing the subject of a formula
L.O To be able to rearrange equations to change the subject using the inverse methods used in linear equations.
In linear equations we solved the problem by working out the value of the term exactly in the problem. However sometimes you may not be able to work out the exact value but instead find the value in terms of another algebraic expression for example:
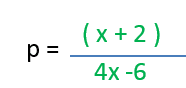

The “subject of a formula” is what the formula is in terms of, with this term appearing on the left hand side of the equation.
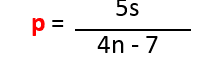
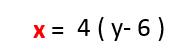
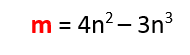



Example 1:
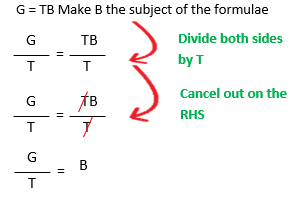
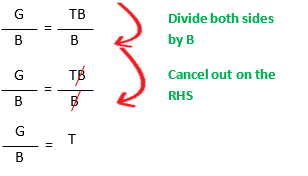
Example 2 :
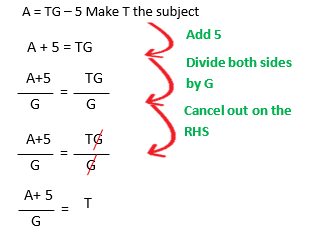

Example 3 : 
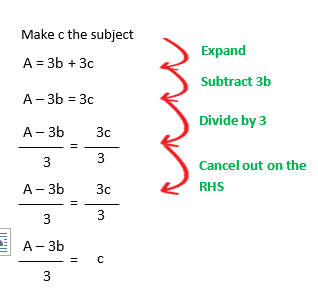

Example 4 :



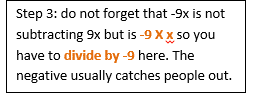
Example 5 :




Word Problems
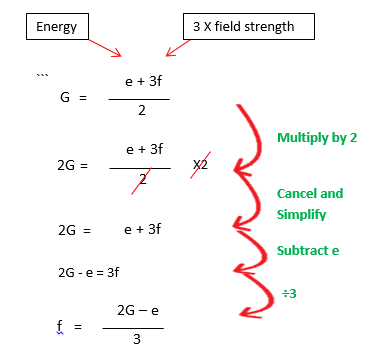
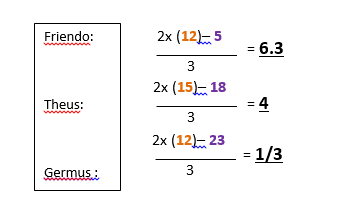
a) Gravitational field strength is denoted by the energy plus three times the field strength divided by 2. However NASA want to work out the field strength on Friendo, Theus and Germus, three theoretical planets.
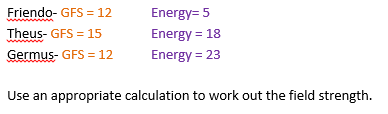




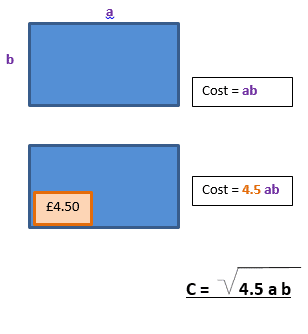
b) Greg is re-carpeting some of the university rooms. The spare room is rectangular shaped and has a widths of 15.5m. He gets a discount which is the same as square rooting the area of the room. The total coast of carpet was £18 costing £4.50 per square metre Work out the length of the room.








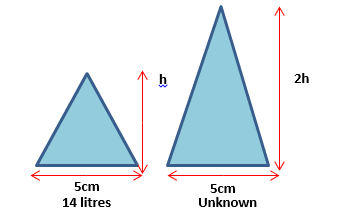
c) Eleanor has a set of 2 cone shaped lava lamps for her bedroom. She has to buy some synthetic liquid to fill them up. The widths of each lava lamp are 5 cm but the heights are different. The larger lamp is 2 times the height of the smaller one. If the small lava lamp requires 14 litres of fluid, how many litres will she need for the larger one? ( 2 d.p accuracy)









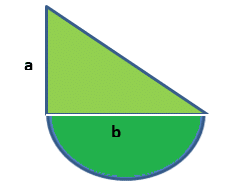
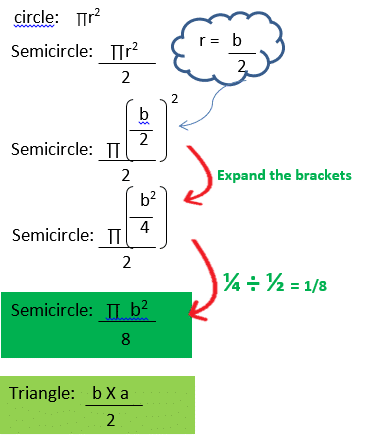
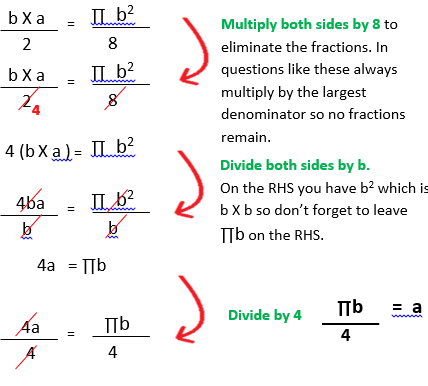
D) Salma draws a cross section of her rose patch in her garden. She simplifies and draws it in the form of a right angled triangle with a semicircle underneath covering the full width. She realises that the areas of both parts of the flower patch are the same. If this is true write a formula expressing the height of the triangle “a” in terms of the full rose patch.