Table of Contents
Unit 1 | Algebra
Page 1 | Expressions and Formulae
Page 3| Solving Linear Equations
Page 4| Expanding and Factorising
Page 5| Factorising Quadratics and expanding double brackets
Page 6| Patterns and Sequences
Page 7| Simultaneous Equations
Page 8| Changing the subject of a Formula
Page 9| Adding , subtracting algebraic formulas
Unit 2 |Graphs
Page 1 | Straight line graphs
Page 2 | Graphs of Quadratic functions
Unit 3 |Geometry and Measure
Page 2 | Symmetry
Page 3 | Coordinates
Page 4 | Perimeter, Area, Volume
Page 6 | Measurement
Page 7 | Trigonometry
Page 8 | Pythagoras
Page 9 | Angles
Page 10 | Shapes
Page 11| Time
Page 12 | Locus
Unit 4 | Numbers
Page 1 | Speed, Distance and time
Page 2 | Rounding and estimating
Page 3 | Ratio and proportion
Page 4 | Factors, Multiples and primes
Page 5 | Powers and roots
Page 7 | Positive and negative numbers
Page 8 | Basic operations
Page 9 | Fractions
Page 10 | Percentages
Unit 5 | Statistics and Probability
Page 1 | Sampling data (MA)
Page 2 | Recording and representing data
Page 3 | Mean median range and mode
Page 4 | Standard deviation
Unit 4 | Calculus
Simultaneous Equations
L.O To be able to solve equations with 2 different variables by satisfying both equations in the problem
When we looked at Linear Equations we were simply working the value of the term in the problem. Notice they were all something like 4p + 10 = 5p – 2 both containing “p” so we could easily solve the problem. What if you received a problem like 4x + y = 15 & 2x + 3y = 10 . How would you tackle this when you would still have the variables “x” and “y” left at the end? This is where simultaneous equations come in.
Example 1: Solve the simultaneous equations
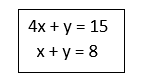
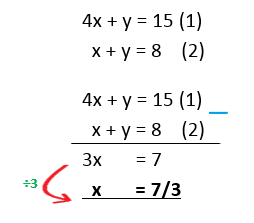
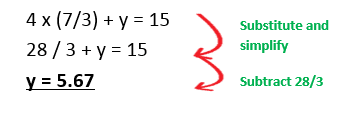



Example 2 : Solve the simultaneous equations
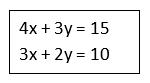
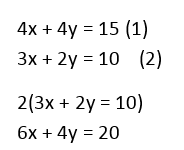




Example 3 : Solve the simultaneous equations
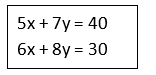
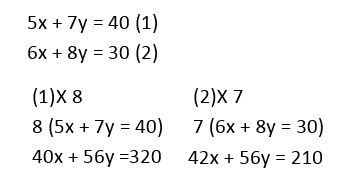
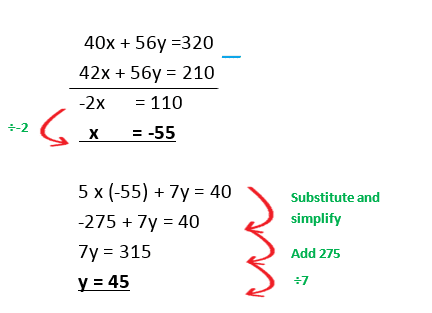



Example 4 : Solve the simultaneous equations
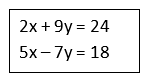
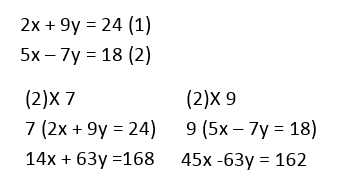
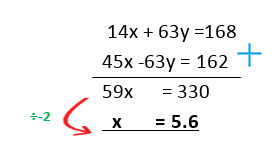
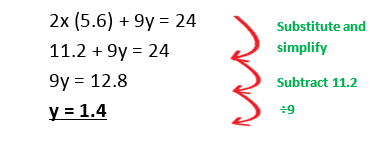




Writing Simultaneous Equations
In many problems you will also have to write out the simultaneous equations out themselves. These can be more challenging at the start but is simply algebraic equations with a context.
Word Problems
a) Alison goes stationary shopping before university. She buys 7 sharpeners and 4 rubbers that cost her £5.00, and then she buys 3 sharpeners and 2 rubbers that cost her £2.00. Work out the cost of a sharpener and rubber each and calculate how much it would be to buy 5 sharpeners and 6 rubbers.







b) Billy is going to university and is taking large boxes (x) and small boxes (y) . He wants to know if they will all fit on his wall. When he takes away the length of a small box from a large box he gets 2m. However when he stacks 2 large boxes and 1 small box he gets a total of 10m. Work out the length of a small box and a large box and how many of each he could fit on an 8 m wall.
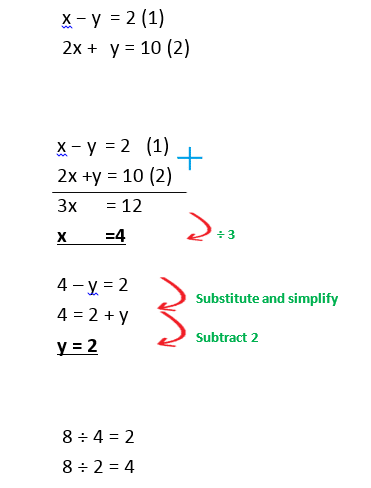




 He can fit 4 small boxes and 2 large boxes
He can fit 4 small boxes and 2 large boxes
c) Ellie is collecting stamps and coins. She places them all on a page in her book. She rearranges one of the lines by taking off 2 coins, so she is only left with 6 stamps which comes to a total of 33 cm. On another line she places 4 stamps and 3 coins ; and this comes to 9 cm. Work out the theoretical length of a stamp and a coin. If the length of a page in her book is 50 cm how many of stamps could she stick on the page.
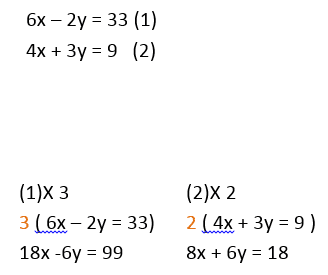

She can fit 11 stamps





c)Mark is playing video games. His characters is collecting gold and silver which his character sells for money. On level 1 he sold 4 gold coins and 3 silver coins for 3 dollars. On level 2 however he sold 6 gold coins and 5 silver coins for 7 dollars. Work out the gamin value of each silver coin and gold coin. How much can he earn if on level 3 he gains 3 gold coins and 6 silver coins?

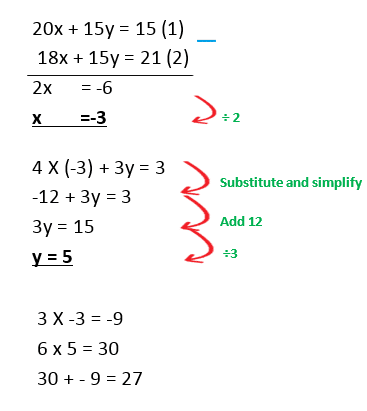
27 dollars






