Fractions

---

L.O- To be able to multiply, divide, add and subtract fractions. Students should also be able to equalise the denominators of fractions and use this in more complicated fraction questions.

Multiplying Fractions

To multiply fractions, simply multiply the top and bottom separately.

Example 1: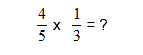

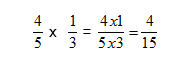
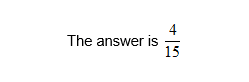
Steps:

Multiply the ‘top numbers’ of the fractions together à this gives you the ‘top number’ of your answer.

Multiply the ‘bottom numbers’ of the fractions together à this gives you the ‘bottom number’ of your answer.

‘top numbers’ = numerators

‘bottom numbers’ = denominators

Dividing Fractions

To divide fractions, turn the 2^nd fraction upside down and then multiply the fractions as normal.

Example 1:

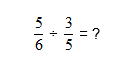
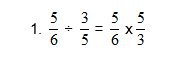
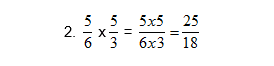
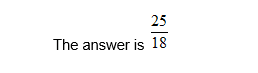
Steps:

1. Turn the 2^nd fraction upside down
2. Now, multiply the two fractions (as done above)

Adding Fractions

To add fractions, you add the top line only but only if the denominators (bottom numbers) are the same.

Example 1: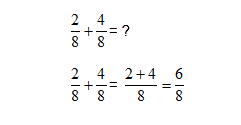

Example 2:

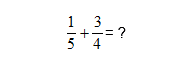
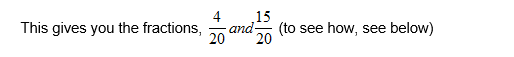
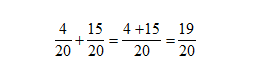
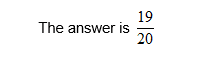
Steps:

Check whether the denominators of the fractions are the same. If they are the same;

• add the ‘top numbers’ of the fractions together à this gives you the top number of your answer
• the bottom number does not change

If they are different  – there is an extra step before you can carry out the main steps.

you will need to equalize the denominators i.e. ‘make the denominators of the fractions the same’

Subtracting Fractions

To subtract fractions, you subtract the top line only, but only if the denominators (bottom numbers) are the same.

Example 1:

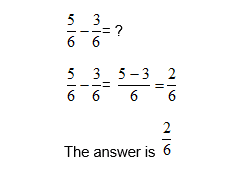
Example 2:

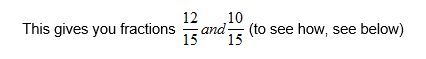
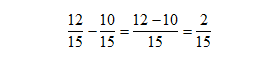
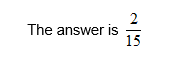
Steps:

Check whether the denominators of the fractions are the same. If they are the same;

• Subtract the ‘top numbers’ of the fractions à this gives you the top number of your answer
• the bottom number does not change

If they are different  – there is an extra step before you can carry out the main steps

• you will need to equalize the denominators FIRST i.e. ‘make the denominators of the fractions the same’

Equalizing the denominator

This means ‘making the denominators of fractions the same.’

This will need to be done during addition/subtraction of fractions when the denominators of the fractions are not the same. It is also done when ordering fractions.

Example 1:

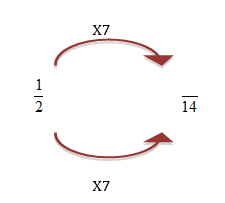
Equalize the denominator of the following fractions

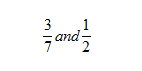
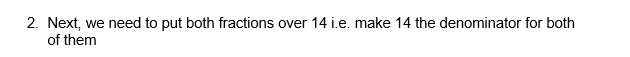
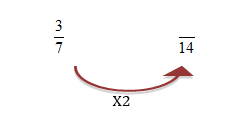
The multiplier in this case is 2

Then, multiply the current numerator by this multiplier

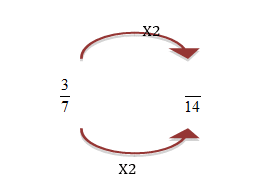
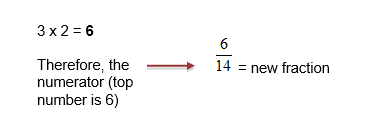
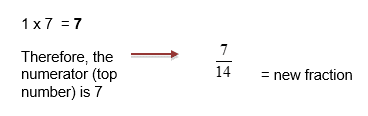
Steps:

1. Find a common denominator of the two fractions.

You can multiply the two denominators together and this will give you a common denominator!

2. Next, we need to put both fractions over 14 i.e. make 14 the denominator for both of them

In order to do this;

• Work out what the current denominator must be multiplied by to become the common denominator. This number is ‘the multiplier’
• Multiply the numerator by this number

This will give you your new fraction.

3. Repeat step 2 for the other fractions in the question.

Here is a question in which you first need to equalize the denominators.

Example 1:

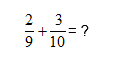
This is an addition (see above).

The denominators are not the same, so first you must equalize the denominators of these true fractions.

The multiplier for the first fraction is 10.

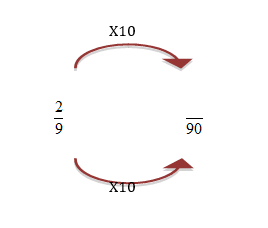
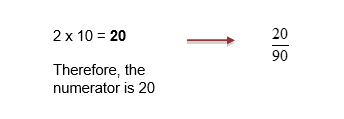
The multiplier for the second fraction is 9.

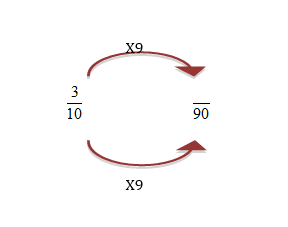
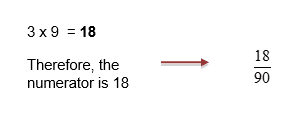
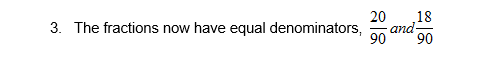
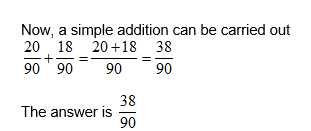
The same method would be carried out if you had to subtract fractions with different denominators.

Ordering fractions

You will need to equalize the denominator for all the fractions before you can put them in order.

Example 1:

Steps:

1. Find a common denominator of the fractions
2. Equalize the denominator of the fractions
3. Place the fractions in the order stated in the question

Remember Ascending order = fractions increase in size

Descending order = fractions decrease in size