Table of Contents
Unit 1 | Algebra
Page 1 | Expressions and Formulae
Page 3| Solving Linear Equations
Page 4| Expanding and Factorising
Page 5| Factorising Quadratics and expanding double brackets
Page 6| Patterns and Sequences
Page 7| Simultaneous Equations
Page 8| Changing the subject of a Formula
Page 9| Adding , subtracting algebraic formulas
Unit 2 |Graphs
Page 1 | Straight line graphs
Page 2 | Graphs of Quadratic functions
Unit 3 |Geometry and Measure
Page 2 | Symmetry
Page 3 | Coordinates
Page 4 | Perimeter, Area, Volume
Page 6 | Measurement
Page 7 | Trigonometry
Page 8 | Pythagoras
Page 9 | Angles
Page 10 | Shapes
Page 11| Time
Page 12 | Locus
Unit 4 | Numbers
Page 1 | Speed, Distance and time
Page 2 | Rounding and estimating
Page 3 | Ratio and proportion
Page 4 | Factors, Multiples and primes
Page 5 | Powers and roots
Page 7 | Positive and negative numbers
Page 8 | Basic operations
Page 9 | Fractions
Page 10 | Percentages
Unit 5 | Statistics and Probability
Page 1 | Sampling data (MA)
Page 2 | Recording and representing data
Page 3 | Mean median range and mode
Page 4 | Standard deviation
Unit 4 | Calculus
Quadratic Equations
L.O To be able to solve quadratic equations through factorising, completing the square and using the quadratic formulae.
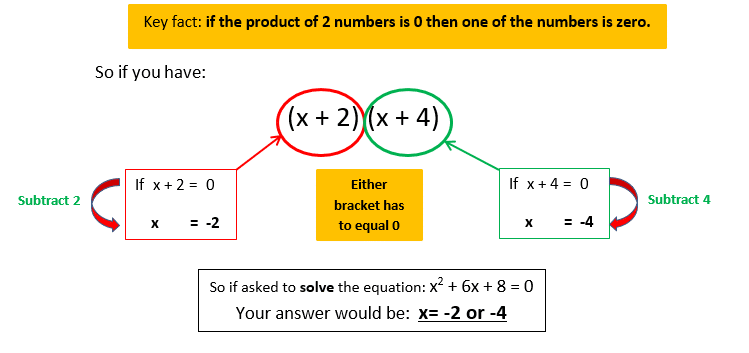
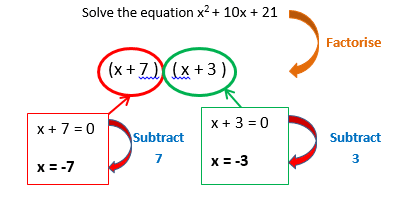
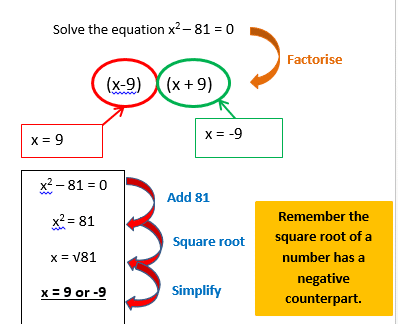
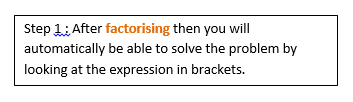
On the previous sheet we learnt how to factorise quadratic equations. If you are told to solve a problem like x2 + 6x + 8 = 0 then the way to tackle it is to factorise first. After factorising you get (x+4) (x+2) = 0 you have to work out different values of x that can go in the brackets that will make the equation work.
Example 1:
Solve the equation x(3x-2)=0
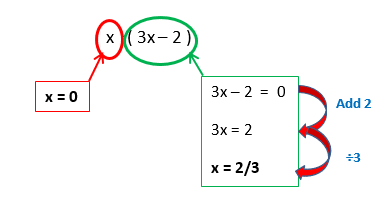
Solve the equation x(3x-2)=0
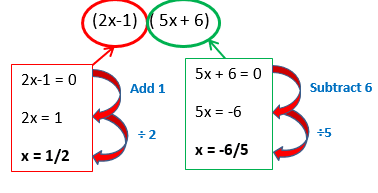


Example 2:

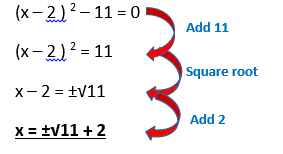
Solving by Completing the Square
Sometime the quadratic equation can’t easily be factorised, in that case you have to “complete the square”, this is denoted by the following equation:
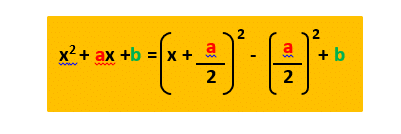
Example 1:
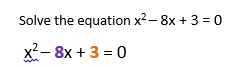
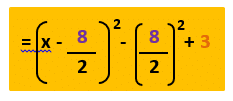
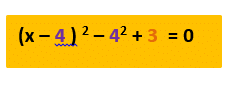
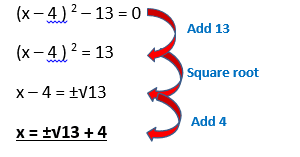



Example 2:
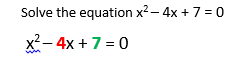
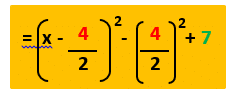
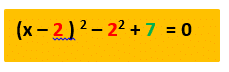



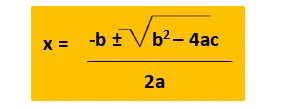
Solving using the Quadratic Formula
In calculator papers you will be expected to use this method of solving quadratic equations. It is simpler than it appears, you have to insert the correct numbers into the correct part of the equation and write the answers to the specified degree of accuracy.
The formula for a quadratic equation in the form ax2 + bx + c is :