Table of Contents
Unit 1 | Algebra
Page 1 | Expressions and Formulae
Page 3| Solving Linear Equations
Page 4| Expanding and Factorising
Page 5| Factorising Quadratics and expanding double brackets
Page 6| Patterns and Sequences
Page 7| Simultaneous Equations
Page 8| Changing the subject of a Formula
Page 9| Adding , subtracting algebraic formulas
Unit 2 |Graphs
Page 1 | Straight line graphs
Page 2 | Graphs of Quadratic functions
Unit 3 |Geometry and Measure
Page 2 | Symmetry
Page 3 | Coordinates
Page 4 | Perimeter, Area, Volume
Page 6 | Measurement
Page 7 | Trigonometry
Page 8 | Pythagoras
Page 9 | Angles
Page 10 | Shapes
Page 11| Time
Page 12 | Locus
Unit 4 | Numbers
Page 1 | Speed, Distance and time
Page 2 | Rounding and estimating
Page 3 | Ratio and proportion
Page 4 | Factors, Multiples and primes
Page 5 | Powers and roots
Page 7 | Positive and negative numbers
Page 8 | Basic operations
Page 9 | Fractions
Page 10 | Percentages
Unit 5 | Statistics and Probability
Page 1 | Sampling data (MA)
Page 2 | Recording and representing data
Page 3 | Mean median range and mode
Page 4 | Standard deviation
Unit 4 | Calculus
Addition Calculations
Some addition calculations can be done in your head, using a mental-method.
In numbers under one hundred, we can just break it down into tens and units and add them separately.
For example, if you had a pair of two-digit–numbers and the units added up to 10, that might easier to do in your head than write down.
Example 1:
Let’s say we got a sum as a question.
56 + 74 =?
We know that 6 + 4 = 10 so all we have to do in our heads is 50 + 70 = 120
Then we can do 120 + 10 = 130 and that’s our answer!
For bigger numbers, it might be easier for us to do a written method of addition. This might be column addition or using a number line.
Example 2:
Let’s use an example so show to use a number line and the column method.
235 + 147 =?
In a number line, we start on the biggest number and count onwards.
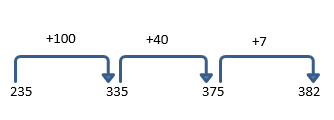
In a column method, first we have to line up the numbers in the correct place value, then add the columns, starting from the left.
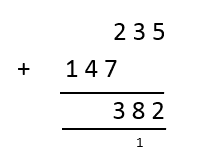
We can also use subtraction to help us work out the answer to an addition question. If there is a question with a missing number (like 6 + ? = 9), we can use the answer and minus the value we do have ( 9 – 6) and we should find our missing value (it’s 3). We can check whether it’s right but
putting the missing value into the original sum and seeing if we get the correct answer. It works with bigger numbers too!
Example 3:
Let’s say that the question we get it 78 +? = 114
We can rearrange this into 114 -78 = ?
The answer is 36!
We can now check this by putting 36 into the original question.
78 + 36 = 114
It works so 36 must be the correct answer.
Addition Calculations Exercise


1) Calculate
a) 23+24+25
b) 425+159
c) 11.6+1.74
[bg_collapse view=”link” color=”#fafafa” expand_text=”Reveal Answer” collapse_text=”Hide Answer” inline_css=”background: #2ea3f2; padding: 9px; font-size: 14px; font-weight: 600;” ][/bg_collapse]
 2)
2)
a) 87 + = 124
b) 3 + 7 = 100
c) 350 – = 117
[bg_collapse view=”link” color=”#fafafa” expand_text=”Reveal Answer” collapse_text=”Hide Answer” inline_css=”background: #2ea3f2; padding: 9px; font-size: 14px; font-weight: 600;” ][/bg_collapse]
 3) Which pair of number will add up to make 100?
3) Which pair of number will add up to make 100?
81 12 29 19 74 42
[bg_collapse view=”link” color=”#fafafa” expand_text=”Reveal Answer” collapse_text=”Hide Answer” inline_css=”background: #2ea3f2; padding: 9px; font-size: 14px; font-weight: 600;” ][/bg_collapse]
 4) Write in the missing number so each side of the triangle has a total of 10
4) Write in the missing number so each side of the triangle has a total of 10
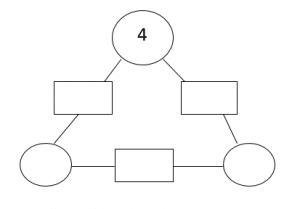
[bg_collapse view=”link” color=”#fafafa” expand_text=”Reveal Answer” collapse_text=”Hide Answer” inline_css=”background: #2ea3f2; padding: 9px; font-size: 14px; font-weight: 600;” ][/bg_collapse]
 5) Write in the number 5,6,7,9 to complete the calculation.
5) Write in the number 5,6,7,9 to complete the calculation.
4
+ 3 6
2 2
[bg_collapse view=”link” color=”#fafafa” expand_text=”Reveal Answer” collapse_text=”Hide Answer” inline_css=”background: #2ea3f2; padding: 9px; font-size: 14px; font-weight: 600;” ][/bg_collapse]

