Table of Contents
Unit 1 | Algebra
Page 1 | Expressions and Formulae
Page 3| Solving Linear Equations
Page 4| Expanding and Factorising
Page 5| Factorising Quadratics and expanding double brackets
Page 6| Patterns and Sequences
Page 7| Simultaneous Equations
Page 8| Changing the subject of a Formula
Page 9| Adding , subtracting algebraic formulas
Unit 2 |Graphs
Page 1 | Straight line graphs
Page 2 | Graphs of Quadratic functions
Unit 3 |Geometry and Measure
Page 2 | Symmetry
Page 3 | Coordinates
Page 4 | Perimeter, Area, Volume
Page 6 | Measurement
Page 7 | Trigonometry
Page 8 | Pythagoras
Page 9 | Angles
Page 10 | Shapes
Page 11| Time
Page 12 | Locus
Unit 4 | Numbers
Page 1 | Speed, Distance and time
Page 2 | Rounding and estimating
Page 3 | Ratio and proportion
Page 4 | Factors, Multiples and primes
Page 5 | Powers and roots
Page 7 | Positive and negative numbers
Page 8 | Basic operations
Page 9 | Fractions
Page 10 | Percentages
Unit 5 | Statistics and Probability
Page 1 | Sampling data (MA)
Page 2 | Recording and representing data
Page 3 | Mean median range and mode
Page 4 | Standard deviation
Unit 4 | Calculus
Table of Contents
Algebra | Unit 1 | Expressions and Formula
Page 3| Changing the Subject of a Formula
Algebra | Unit 2 | Inequalities
Page 1 | Number Lines
Page 2 | Solving Inequalities
Algebra | Unit 3 | Equations
Page 2 | Equations with Brackets
Page 3 | Equations with Fractions
Algebra | Unit 4 | Graphs
Page 1 | Straight Line Graphs ( y = mx + c )
Algebra | Unit 5 | Patterns and Sequences
Page 1 | Basic Patterns
Page 2 | Linear Sequences & nth term
Page 3 | Quadratic Equations
Shape, Space and Measure | Unit 1 |Transformations
Page 1 | Congruent Shapes
Page 2 | Translations
Page 3 | Rotations
Page 4 | Reflections
Page 5 | Enlargements
Shape, Space and Measure | Unit 2 |Symmetry
Page 1 | Line Symmetry
Page 2 | Rotational Symmetry
Shape, Space and Measure | Unit 2 |Coordinates
Page 1 | Plotting Coordinates
Shape, Space and Measure | Unit 3 |Perimeter, Area, Volume
Shape, Space and Measure | Unit 4 |Measurement
Page 1 | Estimation and Accuracy
Page 2 | Scales
Page 3 | Conversions (Metric & Imperial)
Page 4 | Area and Volume Unit Conversions
Shape, Space and Measure | Unit 5 |Trigonometry
Page 1 | Triangle Construction
Shape, Space and Measure | Unit 6 |Pythagoras
Page 1 | Pythagoras Theorem
Page 2 | Line Segments
Shape, Space and Measure | Unit 7 |Angles
Page 1 | Summary of Drawing &Reading Angles
Page 2 | Angle Sum in Different Shapes
Page 3 | Angles in a Polygon
Page 4 | Angles and Parallel Lines
Page 5 | Perpendicular Bisectors
Page 6 | Angle Bisectors
Page 7 | Constructing Loci
Shape, Space and Measure | Unit 8 |Shapes
Page 1 | Properties of Circles
Page 2 | Properties of Polygons
Page 3 | Properties of Triangles
Page 4 | 3D Shapes: Nets & Faces
Shape, Space and Measure | Unit 8 |Time
Page 1 | Units of Time
Page 2 | 12 & 24 Hour Clocks
Page 3 | Timetables
Number | Unit 1 |Place Value
Number | Unit 2 |Distance, Speed and Time
Number | Unit 3 |Rounding and estimating
Number | Unit 4 |Ratio and Proportion
Page 1 | Equivalent Ratios
Page 2 | Division with Ratios
Page 3 | Scale Drawings & Maps
Page 4 | Proportions
Number | Unit 5 |Primer numbers, factors and multiples
Number | Unit 6 |Powers and roots
Number | Unit 7 |Decimals
Page 1 | X 10, 100 & 1000
Page 2 | ÷10, 100 & 1000
Page 3 | Multiplying and Dividing by Whole Numbers
Number | Unit 8 |Positive and negative numbers
Page 1 | Operations with Positive and Negative Numbers
Number | Unit 9 |Operations
Page 1 | BIDMAS Rule
Page 2 | Multiplication & Division (Different Methods)
Page 3 | Converting Fractions, Decimals & Percentages
Number | Unit 10 |Fractions
Page 1 | Equivalent Fractions
Page 2 | Simplifying Fractions
Page 3 | Mixed Numbers
Page 4 | Improper Fractions
Page 5 | Ordering Fractions
Page 6 | Addition & Subtraction
Page 7 | Multiplication & Division
Number | Unit 11 |Percentages
Page 1 | Percentages of Quantities
Page 2 | Interest, Wages & Quantities
Number | Unit 12 |Standard Index form
Page 1 | Decimals in Standard Form
Page 2 | Writing in Standard Form
Page 3 | Addition and Subtraction un Standard Form
Page 4 | Multiplication and Division in Standard Form
Handling Data | Unit 1 |Collecting & Recording Data Representing Data
Page 1 | Tables & Tally Diagrams
Page 2 | Frequency Tables
Page 3 | Stem & Leaf Diagrams
Handling Data | Unit 2 |Representing Data
Page 1 | Bar Charts
Page 2 | Line Graphs
Page 3 | Pictograms
Page 4 | Frequency Polygons
Page 5 | Scatter Diagrams
Page 6 | Pie Charts
Handling Data | Unit 2 |Averages
Page 1 | Mean, Median, Mode & Range
Page 2 | Averages of Grouped Data
Handling Data | Unit 2 |Probability
Page 1 | Basic Probability
Page 2 | Sum of Probabilities
Page 3 | Probability of Combined Events
Division Calculations
Knowing your times tables is very useful when dividing – since division is the inverse of multiplication. For simpler questions, you may want to use certain mental methods when dividing.
Example 1:
If you’re dividing by slightly difficult number, you can break it down to make it easier.
Let’s say that the question is 112 ÷ 14
14 might be difficult to divide by mentally but, we know that 2 x 7 = 14. So, what we can do is divide 112 by 2 first, which is 56. Then we can divide 56 by 7 which is 8.
By breaking it down, the question became much easier and we now know that 112 ÷ 14 = 8.
If a number doesn’t divide completely, you may end up with a remainder at the end. For example, 12÷ 5 wouldn’t fit fully so the answer would be 2 remainder 2, because 2 fives fit into 12 with 2 left over.
With decimals, the way to divide is very similar to the method used in multiplication. You multiply it by 10 or 100 to get a whole number, do the division, then divide your answer by what you multiplied in the beginning.
Example 2:
Let’s say our question is 5.4 ÷ 9
We multiply 5.4 by 10 to get 54.
54 ÷ 9 = 6
We then divide 6 by 10 to get 0.6 à 5.4 ÷ 9 = 0.6
For more complicated division questions, you might want to use a written method such as long division. This involves subtracting multiples of the number you are dividing by.
Example 3:
Let’s say the question is 476 ÷ 19. This is how it would look in long division style.
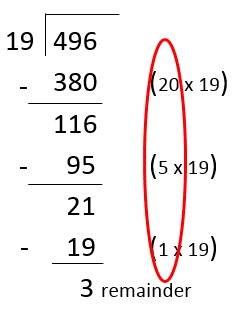

1) Circle the question which have the answer 3
18÷6 27÷9 44÷11
21÷3 45÷9
2) Add in the missing value
72÷![]() = 6
= 6
3) Laura writes a number on paper.She tells James to attend at guessing the number she gives him clue saying. If i divide the number by 9 if equals 13.
What is the number on the paper?![]()
4)
1328 ÷ 4 =![]()
5) 7 × 28 = 196
Use this to calculate 196 ÷ 28 =![]()
6) At a supermarket, a bag can carry a maximum of 6 items. There are 72 items. How many bags can Robert fill?![]()
7) Sams tutor has challenged him to work out
288÷16 288÷2=144 144÷18=8
How can use these two expressions to calculate the answer.
8) A cricket club is travelling to match. there are 17 people on the team.Each can carry 4 people.How many caws will we need?![]()
9) Write the missing signs.
54 ÷9 = 36 ÷![]()

