Table of Contents
Unit 1 | Algebra
Page 1 | Expressions and Formulae
Page 3| Solving Linear Equations
Page 4| Expanding and Factorising
Page 5| Factorising Quadratics and expanding double brackets
Page 6| Patterns and Sequences
Page 7| Simultaneous Equations
Page 8| Changing the subject of a Formula
Page 9| Adding , subtracting algebraic formulas
Unit 2 |Graphs
Page 1 | Straight line graphs
Page 2 | Graphs of Quadratic functions
Unit 3 |Geometry and Measure
Page 2 | Symmetry
Page 3 | Coordinates
Page 4 | Perimeter, Area, Volume
Page 6 | Measurement
Page 7 | Trigonometry
Page 8 | Pythagoras
Page 9 | Angles
Page 10 | Shapes
Page 11| Time
Page 12 | Locus
Unit 4 | Numbers
Page 1 | Speed, Distance and time
Page 2 | Rounding and estimating
Page 3 | Ratio and proportion
Page 4 | Factors, Multiples and primes
Page 5 | Powers and roots
Page 7 | Positive and negative numbers
Page 8 | Basic operations
Page 9 | Fractions
Page 10 | Percentages
Unit 5 | Statistics and Probability
Page 1 | Sampling data (MA)
Page 2 | Recording and representing data
Page 3 | Mean median range and mode
Page 4 | Standard deviation
Unit 4 | Calculus
Probability
We use probability to figure out how likely it is that something will happen. For example, for people who live in Britain, it is very likely that it will rain in September. But it you live in the middle of the Sahara Desert, it is very unlikely that it will rain in September (or any other time of year!).
Many events will have more than one outcome – if you roll a dice, it could land on 1, 2, 3, 4, 5 or 6 – so we use probability to help us guess which outcome is going to happen.
If there is an equally likely chance of things happening, then we say that there is an even chance.
We can use words and fractions to show the probability of something happening. However, if we’re writing probability as a fraction, it’s important to remember that these probabilities can only be between 0 and 1. 0 is impossible and 1 is certain and we can’t have a chance that something is going to happen as less than impossible or more than certain. An even chance of two things happening is written as ½ .
Example 1:
If we use our dice example again, we can show words and fractions can be used to show probability. Let’s say that we want to find out the probability of rolling a two.
There are six possible outcomes of rolling a dice – that it will land on 1, 2, 3, 4, 5 or 6 – and there’s only one of these outcomes that we can roll two. So, the probability of rolling a two is 1 in 6.
If we want to write this as a fraction, the number of possible outcomes becomes the denominator and the number of ways to get the outcome we want is the numerator. So, as a fraction, the probability of rolling a two is .
Therefore, when trying to find probability as a fraction, you must first find all the different outcomes that could possibly happen, and then find how many of those different outcomes are the outcome that you are trying to find.
1)

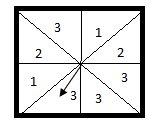

2) A box contains 20 green counters. How many blue counters must be added to the box so theres an equal chance of picking a green counter?![]()
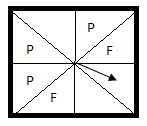
3) Sajid is making a gane.He has marked some number on a spinner .
a) Using only the letters P and F, Write in the empty section so theres a greater chance of landing on a F than a P.
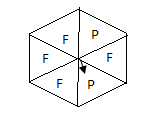
 b) Sajid has made another spinner ,Sajid think there a greater chance of landing of landing on a P than F.is he correct?
b) Sajid has made another spinner ,Sajid think there a greater chance of landing of landing on a P than F.is he correct?
Explain why?
4) Gulam has sacks of potatoes. The probability of selecting a rotten potato from sake A is 3/10.
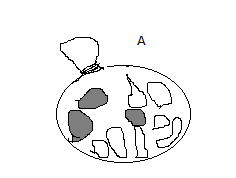
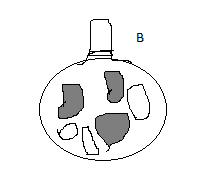
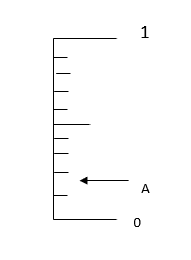
a) Mark on the scale ,the probability of selecting a potato from sack b.
b) How many rotten potatoes should be added to sack C in order for the probability of selecting a rotten potato equals 1/3 =![]()